
分析 判断三角形PF1F2是直角三角形,依题意可求得|PF1|与|PF2|,求出a,然后求解b,即可求解椭圆方程.
解答 解:F1,F2分别是椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左、右焦点,点P在椭圆C上,若线段PF1的中点在y轴上,可得PF2⊥F1F2,∠PF1F2=30°,
∴|F1F2|=2,|PF1|=$\frac{4\sqrt{3}}{3}$,|PF2|=$\frac{2\sqrt{3}}{3}$
又|PF1|+|PF2|=2a=2$\sqrt{3}$,a=$\sqrt{3}$,|F1F2|=2c=2,c=1,
∴b=$\sqrt{2}$.
所求椭圆方程为:$\frac{{x}^{2}}{3}+\frac{{y}^{2}}{2}=1$.
故答案为:$\frac{{x}^{2}}{3}+\frac{{y}^{2}}{2}=1$.
点评 本题考查椭圆的简单性质,求得|PF1|与|PF2|是关键,考查理解与应用能力,属于中档题.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:高中数学 来源: 题型:解答题
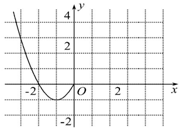 已知函数f(x)是定义在R上的偶函数,现已画出函数f(x)在y轴左侧的图象(二次函数图象的一部分),如图所示,请根据图象:
已知函数f(x)是定义在R上的偶函数,现已画出函数f(x)在y轴左侧的图象(二次函数图象的一部分),如图所示,请根据图象:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{i}{5}$ | B. | $-\frac{1}{5}$ | C. | $\frac{i}{5}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
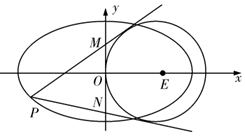 已知椭圆C中心在原点,离心率$\frac{{\sqrt{2}}}{2}$,其右焦点是圆E:(x-1)2+y2=1的圆心.
已知椭圆C中心在原点,离心率$\frac{{\sqrt{2}}}{2}$,其右焦点是圆E:(x-1)2+y2=1的圆心.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 11 | B. | 13 | C. | 17 | D. | 19 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有极大值,无极小值 | B. | 有极小值,无极大值 | ||
| C. | 既有极大值又有极小值 | D. | 既无极大值也无极小值 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com