
分析 当sin(2x+$\frac{π}{6}$)=1时,求出自变量x的集合,此时y=3sin(2x+$\frac{π}{6}$)+1取得最大值;
当sin(2x+$\frac{π}{6}$)=-1时,求出自变量x的集合,此时y=3sin(2x+$\frac{π}{6}$)+1取得最小值.
解答 解:当sin(2x+$\frac{π}{6}$)=1,即自变量x的集合为:
{x|2x+$\frac{π}{6}$=2kπ+$\frac{π}{2}$,k∈z}={x|x=$\frac{π}{6}$+kπ,k∈z} 时,
函数y=3sin(2x+$\frac{π}{6}$)+1取得最大值4;
当sin(2x+$\frac{π}{6}$)=-1,即自变量x的集合为:
{x|2x+$\frac{π}{6}$=2kπ-$\frac{π}{2}$,k∈z}={x|x=-$\frac{π}{3}$+kπ,k∈z} 时,
函数y=3sin(2x+$\frac{π}{6}$)+1取得最小值-2.
点评 本题主要考查了正弦函数的图象与性质的应用问题,是基础题目.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | 1 | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
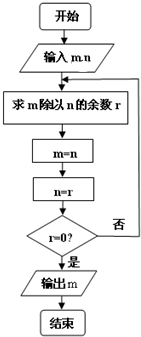 如图程序框图的算法思路来源于我国古代数学名著《九章算术》中的“辗转相除法”,执行该程序框图,若输入的m,n分别为112,91,则输出的m为( )
如图程序框图的算法思路来源于我国古代数学名著《九章算术》中的“辗转相除法”,执行该程序框图,若输入的m,n分别为112,91,则输出的m为( )| A. | 3 | B. | 7 | C. | 0 | D. | 21 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$$\root{3}{18}$ | B. | $\frac{3}{2}$ | C. | $\root{3}{18}$ | D. | $\frac{2}{3}$$\root{3}{18}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com