
���� ��1�������������Ķ�������жϣ�
��2�����ݸ����������֮��Ĺ�ϵ�����жϣ�
��3������ȫ������Ķ�������ʽ����жϣ�
��4������ָ����������������ʽ����жϣ�
��� �⣺��1�����⡰�ڡ�ABC�У���A=30�㣬��sinA=$\frac{1}{2}$�����������Ϊ���ڡ�ABC�У���sinA��$\frac{1}{2}$����A��30�㡱��ȷ���ʣ�1����ȷ��
��2����p��qΪ�����⣬��p��q������һ��Ϊ�����⣬�ʣ�2������
��3��?x��R��sin2x+cos2x=1��������ķ�Ϊ�����⣬�ʣ�3������
��4����֪����p������y=ax-1+2��a��0��a��1����ͼ����һ����A����x-1=0��x=1��
��y=1+2=3�����A������Ϊ��1��3�����ʣ�4������
����ȷ���ǣ�1����
�ʴ�Ϊ����1��
���� ������Ҫ�������������жϣ������������⣬�����������ٹ�ϵ���Լ����������ʣ��漰��֪ʶ��϶࣬�ۺ��Խ�ǿ�����ѶȲ���


 ����ν����Ž̲��㽭���̴�ѧ������ϵ�д�
����ν����Ž̲��㽭���̴�ѧ������ϵ�д� �����Ļ������������������ϵ�д�
�����Ļ������������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $y=\sqrt{{x^2}-1}$ | B�� | y=x2 | C�� | y=2x | D�� | y=lnx |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
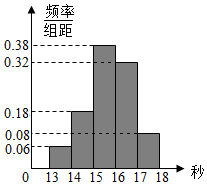 ij��50��ѧ����һ�ΰ��ײ����У��ɼ�ȫ������13����18��֮�䣬�����Խ����
ij��50��ѧ����һ�ΰ��ײ����У��ɼ�ȫ������13����18��֮�䣬�����Խ�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֶ�����Ҫ���� | B�� | ��Ҫ����������� | ||
| C�� | ��Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com