
选修4﹣2:矩阵与变换
已知二阶矩阵A=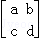 ,矩阵A属于特征值λ1=﹣1的一个特征向量为α1=
,矩阵A属于特征值λ1=﹣1的一个特征向量为α1=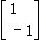 ,属于特征值λ2=4的一个特征向量为α2=
,属于特征值λ2=4的一个特征向量为α2= .求矩阵A.
.求矩阵A.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:[同步]2014年新人教A版选修4-5 1.2绝对值不等式练习卷(解析版) 题型:选择题
(2012•甘肃一模)若不等式|x﹣a|<1成立的充分非必要条件是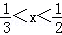 则实数a的取值范围是( )
则实数a的取值范围是( )
A.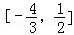 B.
B.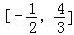 C.
C.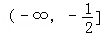 D.
D.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-5 1.1不等式练习卷(解析版) 题型:选择题
(2014•榆林模拟)已知各项均为正数的等比数列{an}满足a7=a6+2a5,若存在两项am,an使得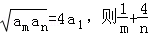 的最小值为( )
的最小值为( )
A. B.
B.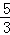 C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-2 4.2特征向量的应用练习卷(解析版) 题型:解答题
选修4﹣2:矩阵与变换
已知二阶矩阵M有特征值λ1=4及属于特征值4的一个特征向量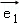 =(
=(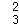 ),并有特征值λ2=﹣1及属于特征值﹣1的一个特征向量
),并有特征值λ2=﹣1及属于特征值﹣1的一个特征向量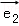 =(
=(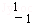 ),
),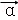 =(
=(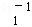 ).
).
(1)求矩阵M;
(2)求M5α.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-2 4.2特征向量的应用练习卷(解析版) 题型:解答题
选修4﹣2:矩阵与变换
给定矩阵A= ,B=
,B= .
.
(1)求A的特征值λ1,λ2及对应特征向量α1,α2,
(2)求A4B.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-2 4.2特征向量的应用练习卷(解析版) 题型:解答题
(2014•盐城二模)已知矩阵A=[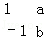 ]的一个特征值为2,其对应的一个特征向量为
]的一个特征值为2,其对应的一个特征向量为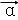 =[
=[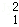 ].
].
(1)求矩阵A;
(2)若A[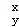 ]=[
]=[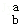 ],求x,y的值.
],求x,y的值.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-2 3.3逆矩阵与二元一次方程组(解析版) 题型:填空题
(2013•杨浦区一模)若线性方程组的增广矩阵为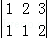 ,则该线性方程组的解是 .
,则该线性方程组的解是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com