
分析 利用同角三角函数基本关系式求解正弦函数以及余弦函数,正切函数的值,化简所求表达式求解即可.
解答 解:∵$x∈(-\frac{π}{2},0)$,$cos(\frac{π}{2}+x)=\frac{4}{5}$,∴$sinx=-\frac{4}{5},cosx=\frac{3}{5},tanx=-\frac{4}{3}$,
∴$\frac{{sin2x-2{{sin}^2}x}}{1+tanx}=\frac{{2sinxcosx-2{{sin}^2}x}}{{1+\frac{sinx}{cosx}}}=\frac{2sinxcosx(cosx-sinx)}{cosx+sinx}=\frac{168}{25}$.
点评 本题考查三角函数的化简求值,同角三角函数基本关系式的应用,考查计算能力.


科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{3}$ | B. | 2 | C. | -$\frac{2}{3}$ | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 设α、β为两个不同平面,若直线l在平面α内,则“α⊥β”是“l⊥β”的必要不充分条件 | |
| B. | 设随机变量ξ服从正态分布N(0,1),若P(ξ>1)=p,则P(-1<ξ<0)=$\frac{1}{2}$-p | |
| C. | 要得到函数f(x)=cos(2x+$\frac{π}{3}}$)的图象,只需将函数g(x)=sin(2x+$\frac{π}{3}}$)的图象向左平移$\frac{π}{4}$个单位长度 | |
| D. | ?x∈(0,$\frac{π}{2}$),x<sinx |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若向量$\overrightarrow{a}$∥$\overrightarrow{b}$,则存在唯一的实数λ使得$\overrightarrow a$=λ$\overrightarrow b$ | |
| B. | 命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1” | |
| C. | 命题“?x0∈R,使得x02+x0+1<0”的否定是:“?x∈R,均有x2+x+1>0” | |
| D. | “a≠5且b≠-5”是“a+b≠0”的不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
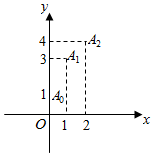 若k≠0,n是大于1的自然数,二项式(1+$\frac{x}{k}$)n的展开式为a0+a1x+a2x2+a3x3+a4x4…+anxn.若点Ai(i,ai)(i=0,1,2)的位置如图所示,则${∫}_{-1}^{k}$x2dx的值为( )
若k≠0,n是大于1的自然数,二项式(1+$\frac{x}{k}$)n的展开式为a0+a1x+a2x2+a3x3+a4x4…+anxn.若点Ai(i,ai)(i=0,1,2)的位置如图所示,则${∫}_{-1}^{k}$x2dx的值为( )| A. | $\frac{28}{3}$ | B. | $\frac{26}{3}$ | C. | 28 | D. | 26 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 已知数列{an}满足a1=1,a2=$\frac{1}{2}$,且an+2=$\frac{{{a}_{n+1}}^{2}}{{a}_{n}+{a}_{n+1}}$(n∈N*),则如图中第10行所有数的和为2046.
已知数列{an}满足a1=1,a2=$\frac{1}{2}$,且an+2=$\frac{{{a}_{n+1}}^{2}}{{a}_{n}+{a}_{n+1}}$(n∈N*),则如图中第10行所有数的和为2046.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com