
 已知数列{an}满足a1=1,a2=$\frac{1}{2}$,且an+2=$\frac{{{a}_{n+1}}^{2}}{{a}_{n}+{a}_{n+1}}$(n∈N*),则如图中第10行所有数的和为2046.
已知数列{an}满足a1=1,a2=$\frac{1}{2}$,且an+2=$\frac{{{a}_{n+1}}^{2}}{{a}_{n}+{a}_{n+1}}$(n∈N*),则如图中第10行所有数的和为2046. 分析 由${a_{n+2}}=\frac{{a_{n+1}^2}}{{{a_n}+{a_{n+1}}}}$得,$\frac{{{a_{n+2}}}}{{{a_{n+1}}}}=\frac{{a_{n+1}^{\;}}}{{{a_n}+{a_{n+1}}}}$,两边取倒数得$\frac{{{a_{n+1}}}}{{{a_{n+2}}}}=\frac{{a_n^{\;}}}{{{a_{n+1}}}}+1$,利用等差数列的通项公式可得:$\frac{a_n}{{{a_{n+1}}}}=n+1$,由累乖法可得${a_n}=\frac{1}{n!}$,可得$\frac{{{a_i}{a_{n+1-i}}}}{{{a_{n+1}}}}$=$\frac{(n+1)!}{i!(n+1-i)!}=C_{n+1}^i$,即可得出.
解答 解:由${a_{n+2}}=\frac{{a_{n+1}^2}}{{{a_n}+{a_{n+1}}}}$得,$\frac{{{a_{n+2}}}}{{{a_{n+1}}}}=\frac{{a_{n+1}^{\;}}}{{{a_n}+{a_{n+1}}}}$,
∴两边取倒数得$\frac{{{a_{n+1}}}}{{{a_{n+2}}}}=\frac{{a_n^{\;}}}{{{a_{n+1}}}}+1$,
∴数列$\{\frac{a_n}{{{a_{n+1}}}}\}$是以$\frac{a_1}{a_2}=2$为首项,以1为公差的等差数列,
∴$\frac{a_n}{{{a_{n+1}}}}=n+1$,∴由累乘法可得${a_n}=\frac{1}{n!}$,
∴$\frac{{{a_i}{a_{n+1-i}}}}{{{a_{n+1}}}}$=$\frac{(n+1)!}{i!(n+1-i)!}=C_{n+1}^i$
图中第10行所有数的和为$\frac{{{a_1}{a_{10}}}}{{{a_{11}}}}$+$\frac{{{a_2}{a_9}}}{{{a_{11}}}}$+$\frac{{{a_3}{a_8}}}{{{a_{11}}}}$+…+$\frac{{{a_8}{a_3}}}{{{a_{11}}}}$+$\frac{{{a_9}{a_2}}}{{{a_{11}}}}$+$\frac{{{a_{10}}{a_1}}}{{{a_{11}}}}$
=$C_{11}^1+C_{11}^2+C_{11}^3+…+C_{11}^8+C_{11}^9+C_{11}^{10}$=211-2=2046.
故答案为:2046.
点评 本题考查了等差数列的通项公式、递推关系、组合数的计算公式、“累乘法”,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 6 | C. | $2\sqrt{14}$ | D. | $4\sqrt{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 2 | C. | $\sqrt{5}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
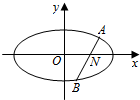 如图,设过点N(1,0)的动直线l交椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)于A,B两点,且|AB|的最小值为1,椭圆C的离心率e=$\frac{\sqrt{3}}{2}$.
如图,设过点N(1,0)的动直线l交椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)于A,B两点,且|AB|的最小值为1,椭圆C的离心率e=$\frac{\sqrt{3}}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com