
| A. | 4 | B. | 6 | C. | $2\sqrt{14}$ | D. | $4\sqrt{7}$ |
分析 根据双曲线的性质求出c的值,结合向量垂直和向量和的几何意义进行转化求解即可.
解答 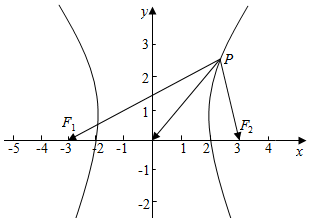 解:由双曲线方程得a2=4,b2=5,c2=9,
解:由双曲线方程得a2=4,b2=5,c2=9,
即c=3,则焦点为F1(-3,0),F2(3,0),
∵点P在双曲线C的右支上,且$\overrightarrow{P{F_1}}$•$\overrightarrow{P{F_2}}$=0,
∴△F1PF2为直角三角形,
则|$\overrightarrow{P{F_1}}$+$\overrightarrow{P{F_2}|}$=|2$\overrightarrow{PO}$|=|F1F2|=2c=6,
故选:B.
点评 本题主要考查双曲线性质的有意义,根据向量垂直和向量和的几何意义是解决本题的关键.


科目:高中数学 来源: 题型:选择题
 如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D,测得∠BCD=75°,∠BDC=60°,CD=40m,并在点C测得塔顶A的仰角为30°.则塔高AB为( )m.
如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D,测得∠BCD=75°,∠BDC=60°,CD=40m,并在点C测得塔顶A的仰角为30°.则塔高AB为( )m.| A. | 20 | B. | 20$\sqrt{2}$ | C. | 20$\sqrt{3}$ | D. | 40 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 设α、β为两个不同平面,若直线l在平面α内,则“α⊥β”是“l⊥β”的必要不充分条件 | |
| B. | 设随机变量ξ服从正态分布N(0,1),若P(ξ>1)=p,则P(-1<ξ<0)=$\frac{1}{2}$-p | |
| C. | 要得到函数f(x)=cos(2x+$\frac{π}{3}}$)的图象,只需将函数g(x)=sin(2x+$\frac{π}{3}}$)的图象向左平移$\frac{π}{4}$个单位长度 | |
| D. | ?x∈(0,$\frac{π}{2}$),x<sinx |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
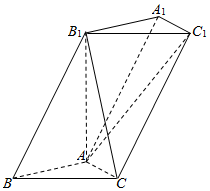 如图,三棱柱ABC-A1B1C1中,底面ABC为等腰直角三角形,AB=AC=1,BB1=2,B1C=2,∠ABB1=60°.
如图,三棱柱ABC-A1B1C1中,底面ABC为等腰直角三角形,AB=AC=1,BB1=2,B1C=2,∠ABB1=60°.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若向量$\overrightarrow{a}$∥$\overrightarrow{b}$,则存在唯一的实数λ使得$\overrightarrow a$=λ$\overrightarrow b$ | |
| B. | 命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1” | |
| C. | 命题“?x0∈R,使得x02+x0+1<0”的否定是:“?x∈R,均有x2+x+1>0” | |
| D. | “a≠5且b≠-5”是“a+b≠0”的不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 已知数列{an}满足a1=1,a2=$\frac{1}{2}$,且an+2=$\frac{{{a}_{n+1}}^{2}}{{a}_{n}+{a}_{n+1}}$(n∈N*),则如图中第10行所有数的和为2046.
已知数列{an}满足a1=1,a2=$\frac{1}{2}$,且an+2=$\frac{{{a}_{n+1}}^{2}}{{a}_{n}+{a}_{n+1}}$(n∈N*),则如图中第10行所有数的和为2046.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com