
���� ��I���ֱ���¼��ס��ҡ����������Ժϸ�Ϊ A��B��C��D��������֪ A��B��C��D���������${P}��{A}��={P}��{B}��=\frac{1}{2}$��${P}��C��={P}��D��=\frac{2}{3}$�����¼���������δǩԼ��ΪF�����¼��Ķ����Ժͻ����Ե������������δǩԼ�ĸ��ʣ�
��II�� X�����п���ȡֵΪ0��1��2��3��4���ֱ������Ӧ�ڵĸ��ʣ��ɴ������X�ķֲ��к�X����ѧ������
��� �⣺��I���ֱ���¼��ס��ҡ����������Ժϸ�Ϊ A��B��C��D��
������֪ A��B��C��D���������${P}��{A}��={P}��{B}��=\frac{1}{2}$��${P}��C��={P}��D��=\frac{2}{3}$��
���¼���������δǩԼ��ΪF��
���¼��Ķ����Ժͻ����Եã�
P��F��=1-P��CD������3�֣�
=$1-\frac{2}{3}��\frac{2}{3}=\frac{5}{9}$����4�֣�
��II�� X�����п���ȡֵΪ0��1��2��3��4������5�֣�
${P}��{{X}=0}��={P}��{\overline{{A}{B}}}��{P}��F��=\frac{1}{2}��\frac{1}{2}��\frac{5}{9}=\frac{5}{36}$��
${P}��{{X}=1}��={P}��{{A}\bar{B}}��{P}��F��+{P}��{\bar{A}{B}}��{P}��F��=2��\frac{1}{2}��\frac{1}{2}��\frac{5}{9}=\frac{5}{18}$��
${P}��{{X}=2}��={P}��{{A}{B}F}��+{P}��{\bar{A}\bar{B}CD}��=\frac{1}{2}��\frac{1}{2}��\frac{5}{9}+\frac{1}{2}��\frac{1}{2}��\frac{2}{3}��\frac{2}{3}=\frac{1}{4}$��
${P}��{{X}=3}��={P}��{{A}\bar{B}CD}��+{P}��{\bar{A}{B}CD}��=2��\frac{1}{2}��\frac{1}{2}��\frac{2}{3}��\frac{2}{3}=\frac{2}{9}$��
${P}��{{X}=4}��={P}��{{A}{B}CD}��=\frac{1}{2}��\frac{1}{2}��\frac{2}{3}��\frac{2}{3}=\frac{1}{9}$��
���ԣ�X�ķֲ����ǣ�
| X | 0 | 1 | 2 | 3 | 4 |
| P | $\frac{5}{36}$ | $\frac{5}{18}$ | $\frac{1}{4}$ | $\frac{2}{9}$ | $\frac{1}{9}$ |
���� ���⿼����ʵ���������ɢ����������ķֲ��к���ѧ�����������е��⣬����ʱҪ�������⣬ע������¼����ʼ��㹫ʽ�ĺ������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {x|x��-1��x��1} | B�� | {x|x��0��x��2} | C�� | {x|x��0��x��1} | D�� | {x|x��0��x��2} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -5��2 | B�� | -1��4 | C�� | -5��4 | D�� | -5��-1��2��4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
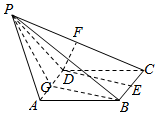 ��ͼ����P-ABCD�У�ABCDΪ�߳�Ϊ1�����Σ��ҡ�DAB=60�㣬PA=PD=$\sqrt{2}$��PB=2��E��F��G�ֱ�ΪBC��PC��AD�е㣮
��ͼ����P-ABCD�У�ABCDΪ�߳�Ϊ1�����Σ��ҡ�DAB=60�㣬PA=PD=$\sqrt{2}$��PB=2��E��F��G�ֱ�ΪBC��PC��AD�е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1008 | B�� | 2015 | C�� | 2016 | D�� | 2017 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com