
分析 根据平面向量的坐标运算与数量积运算,计算即可.
解答 解:向量$\overrightarrow{a}$=(cos15°,sin15°),$\overrightarrow{b}$=(cos75°,sin75°),
∴${\overrightarrow{a}}^{2}$=cos215°+sin215°=1,|$\overrightarrow{a}$|=1;
${\overrightarrow{b}}^{2}$=cos275°+sin275°=1,|$\overrightarrow{b}$|=1;
∴$\overrightarrow{a}$•$\overrightarrow{b}$=cos15°cos75°+sin15°cos75°=cos60°=$\frac{1}{2}$;
${(\overrightarrow{a}-2\overrightarrow{b})}^{2}$=${\overrightarrow{a}}^{2}$-4$\overrightarrow{a}$•$\overrightarrow{b}$+4${\overrightarrow{b}}^{2}$=1-4×$\frac{1}{2}$+4=3,
∴|a-2b|=$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 本题考查了平面向量的坐标运算与数量积运算问题,是基础题目.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -21 | B. | -32 | C. | -2 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
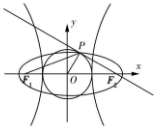 如图,已知双曲线C:$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点分别为F1,F2,离心率为2,以双曲线C的实轴为直径的圆记为圆O,过点F2作圆O的切线,切点为P,则以F1,F2为焦点,过点P的椭圆T的离心率为( )
如图,已知双曲线C:$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点分别为F1,F2,离心率为2,以双曲线C的实轴为直径的圆记为圆O,过点F2作圆O的切线,切点为P,则以F1,F2为焦点,过点P的椭圆T的离心率为( )| A. | $\frac{{\sqrt{5}-\sqrt{3}}}{2}$ | B. | $\sqrt{5}-\sqrt{3}$ | C. | $\frac{{\sqrt{7}-\sqrt{3}}}{4}$ | D. | $\sqrt{7}-\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[e-\frac{1}{e},e)$ | B. | [1,e+1) | C. | [e,e+1) | D. | $(e-\frac{1}{e},e+1)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
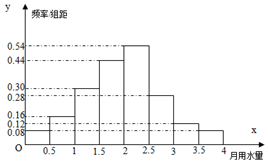 为了了解某小区2000户居民月用水量使用情况,通过随机抽样获得了100户居民的月用水量.如图是调查结果的频率分布直方图.
为了了解某小区2000户居民月用水量使用情况,通过随机抽样获得了100户居民的月用水量.如图是调查结果的频率分布直方图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com