
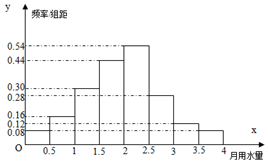
 为了了解某小区2000户居民月用水量使用情况,通过随机抽样获得了100户居民的月用水量.如图是调查结果的频率分布直方图.
为了了解某小区2000户居民月用水量使用情况,通过随机抽样获得了100户居民的月用水量.如图是调查结果的频率分布直方图.分析 (1)根据频率分布图画出频率分布折线图即可;
(2)利用频率、频数与样本容量的关系求出该小区居民月用水量使用大于3的户数;
(3)根据频率分布直方图求出众数与中位数.
解答 解:(1)画出频率分布折线图,如图所示;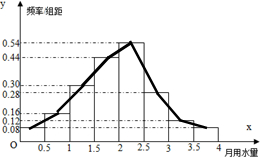 (3分)
(3分)
(2)∵样本中居民月用水量在3-3.5的频率为
f=0.12×0.5=0.06,…(4分)
∵样本中居民月用水量在3.5-4的频率为
f=0.08×0.5=0.04,…(5分)
∴样本中居民月用水量大于3的频率为为
0.06×0.04=0.1;…(6分)
所以某小区2000户居民月用水量使用大于3的户数为
2000×0.1=200;…(7分)
(3)①众数为2.25…(9分)
②中位数为
2+$\frac{0.5-(0.04+0.08+0.15+0.22)}{0.54}$≈2.019;…(11分)
所以该样本的众数为2.25,中位数为2.019…(12分)
点评 本题考查了频率分布直方图与折线图的应用问题,是基础题目.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{18}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 9 | D. | 13 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
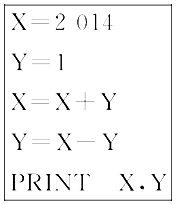
| A. | 2 015,2 013 | B. | 2 013,2 015 | C. | 2 015,2 015 | D. | 2 015,2 014 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com