
分析 由y=$\frac{4}{c}$sin[5(ax+b)+$\frac{π}{4}$]-$\frac{d}{c}$与y=5sin4x+1为同一函数,系数对应相等,求出a,b,c,d的值即可.
解答 解:∵cy+d=4sin(5x+$\frac{π}{4}$),
∴y=$\frac{4}{c}$sin[5(ax+b)+$\frac{π}{4}$]-$\frac{d}{c}$与y=5sin4x+1为同一函数,
∴$\left\{\begin{array}{l}{\frac{4}{c}=5}\\{5a=4}\\{5b+\frac{π}{4}=0}\\{-\frac{d}{c}=1}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=\frac{4}{5}}\\{b=-\frac{π}{20}}\\{c=\frac{4}{5}}\\{d=-\frac{4}{5}}\end{array}\right.$.
点评 本题考查了坐标转化问题,考查三角函数问题以及转化思想,是一道中档题.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:高中数学 来源: 题型:解答题
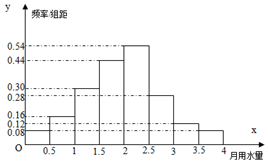 为了了解某小区2000户居民月用水量使用情况,通过随机抽样获得了100户居民的月用水量.如图是调查结果的频率分布直方图.
为了了解某小区2000户居民月用水量使用情况,通过随机抽样获得了100户居民的月用水量.如图是调查结果的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com