
分析 由等差数列的通项公式可知:$\frac{S(n)}{T(n)}$=$\frac{3n+2}{4n+5}$=$\frac{\frac{(3n+2)n}{2}}{\frac{(3n+2)n}{2}}$,分别求得S(n)=$\frac{(3n+2)n}{2}$,T(n)=$\frac{(4n+5)n}{2}$,由平面向量的基本定理可知:$\frac{{a}_{1}+{a}_{4}}{{b}_{3}}$+λ=1,分别求得a1+a4和b3,求得$\frac{{a}_{1}+{a}_{4}}{{b}_{3}}$=$\frac{28}{25}$,即可求得实数λ的值.
解答 解:S(n),T(n)分别为等差数列{an},{bn}的前n项和,
由等差数列前n项和公式可知:$\frac{S(n)}{T(n)}$=$\frac{3n+2}{4n+5}$=$\frac{\frac{(3n+2)n}{2}}{\frac{(3n+2)n}{2}}$,
∴S(n)=$\frac{(3n+2)n}{2}$,T(n)=$\frac{(4n+5)n}{2}$,
∵P是直线BC上一点,
∴$\overrightarrow{BP}$=k$\overrightarrow{BC}$,k∈R,
∴$\overrightarrow{AP}$-$\overrightarrow{AB}$=k($\overrightarrow{AC}$-$\overrightarrow{AB}$),
∴$\overrightarrow{AP}$=(1-k)$\overrightarrow{AB}$+k$\overrightarrow{AC}$,
∵$\overrightarrow{AP}$=$\frac{{{a_1}+{a_4}}}{b_3}$•$\overrightarrow{AB}$+λ•$\overrightarrow{AC}$,
∴$\frac{{a}_{1}+{a}_{4}}{{b}_{3}}$+λ=1,
由S4=$\frac{4×({a}_{1}+{a}_{4})}{2}$=2(a1+a4),
∴a1+a4=$\frac{1}{2}$×S4=14,
b3=$\frac{1}{2}$×(b1+b5)=$\frac{1}{2}$×$\frac{2{T}_{5}}{5}$=$\frac{25}{2}$,
∴$\frac{{a}_{1}+{a}_{4}}{{b}_{3}}$=$\frac{28}{25}$,
λ=1-$\frac{28}{25}$=$-\frac{3}{25}$,
故答案为:$-\frac{3}{25}$.
点评 本题考查等差数列的性质,等差数列前n项公式,考查平面向量的基本定理及其意义,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
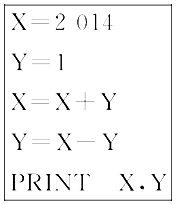
| A. | 2 015,2 013 | B. | 2 013,2 015 | C. | 2 015,2 015 | D. | 2 015,2 014 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,PA⊥CD,AD∥BC,∠ADC=∠PAB=90°,BC=CD=AE=$\frac{1}{2}$AD=1,PA=2.
如图,在四棱锥P-ABCD中,PA⊥CD,AD∥BC,∠ADC=∠PAB=90°,BC=CD=AE=$\frac{1}{2}$AD=1,PA=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com