
 如图ABCD是一块边长为100m的正方形地皮,其中ATPN是一半径为90m的扇形小山,P是弧TN上一点,其余部分都是平地,现一开发商想在平地上建造一个有边落在BC与CD上的长方形停车场PQCR(如图所示),设∠PAB=θ.
如图ABCD是一块边长为100m的正方形地皮,其中ATPN是一半径为90m的扇形小山,P是弧TN上一点,其余部分都是平地,现一开发商想在平地上建造一个有边落在BC与CD上的长方形停车场PQCR(如图所示),设∠PAB=θ.分析 (Ⅰ)先求出AM和PM的值,进而可得PQ,PR 的值,由此求得S=PQ•PR 的值.
(Ⅱ)设sinθ+cosθ=t,则 sinθcosθ=$\frac{{t}^{2}-1}{2}$,代入S化简得 S=$\frac{8100}{2}(t-\frac{10}{9})^{2}+950$,利用二次函数性质求出S的最大值和最小值.
解答 解:(Ⅰ)由于∠PAB=θ,0°≤θ≤90°,
知AM=90cosθ,PM=90sinθ,
RP=RM-PM=100-90sinθ,
PQ=MB=100-90cosθ,
S=PQ•PR=(100-90sinθ )(100-90cosθ )
=10000-9000(sinθ+cosθ)+8100sinθcosθ.
∴S=10000-9000(sinθ+cosθ)+8100sinθcosθ;
(Ⅱ)设sinθ+cosθ=t,则 sinθcosθ=$\frac{{t}^{2}-1}{2}$.
即t=$\sqrt{2}$sin(θ+$\frac{π}{4}$),0≤θ≤$\frac{π}{2}$,1≤t≤$\sqrt{2}$,
代入S化简得 S=$\frac{8100}{2}(t-\frac{10}{9})^{2}+950$.
故当t=$\frac{10}{9}$时,Smin=950(m2);
当t=$\sqrt{2}$时,Smax=14050-9000$\sqrt{2}$(m2).
点评 本题考查解三角形的实际应用,三角函数的恒等变换,以及二次函数性质的应用,属中档题.


科目:高中数学 来源: 题型:解答题
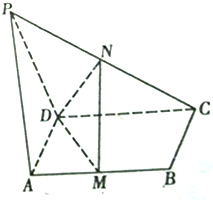 如图,已知PA⊥平面ABCD,ABCD为矩形,M、N为AB、PC的中点.
如图,已知PA⊥平面ABCD,ABCD为矩形,M、N为AB、PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x-y-1=0 | B. | x+y+1=0 | C. | x-y+1=0 | D. | x+y-1=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com