
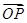 =
=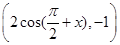 ,
,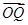 =
=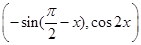 ,定义函数f(x)=
,定义函数f(x)=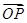 ·
·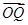 .
.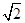 sin
sin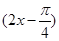 ,f(x)的最大值和最小值分别是
,f(x)的最大值和最小值分别是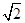 和-
和-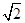 .(2)S=2
.(2)S=2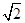 .
.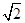 sin
sin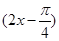 ,由此可得f(x)的最大值和最小值分别为
,由此可得f(x)的最大值和最小值分别为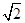 和-
和-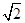 ;(2)由f(A)=1可求得角A,再由三角形面积公式S=
;(2)由f(A)=1可求得角A,再由三角形面积公式S=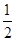 bcsin A即可得其面积.
bcsin A即可得其面积.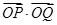 =(-2sin x,-1)·(-cos x,cos 2x)
=(-2sin x,-1)·(-cos x,cos 2x)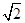 sin
sin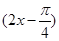 )
)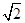 和-
和-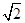
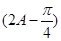 =
=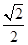 .
.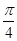 =
=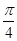 或2A-
或2A-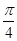 =
=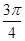 .∴A=
.∴A=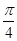 或A=
或A=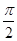 .
.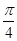 .∵bc=8,
.∵bc=8,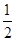 bcsin A=
bcsin A=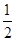 ×8×
×8×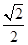 =2
=2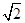


 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源:不详 题型:解答题
 ,
, ,函数
,函数 ,
,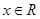 .
.
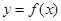 的图像的对称中心坐标;
的图像的对称中心坐标;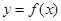 图像向下平移
图像向下平移 个单位,再向左平移
个单位,再向左平移 个单位得函数
个单位得函数 的图像,试写出
的图像,试写出 的解析式并作出它在
的解析式并作出它在 上的图像.
上的图像.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
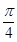 +
+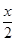 )cos(
)cos(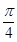 +
+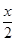 ).(1)若f(α)=
).(1)若f(α)=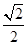 ,α∈(-
,α∈(-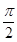 ,0),求α的值;
,0),求α的值;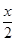 =
=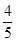 ,x∈(
,x∈(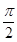 ,π),求f(x)的值.
,π),求f(x)的值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com