
| 日需求量 | 7 | 8 | 9 | 10 | 11 | 12 |
| 频数 | 4 | 8 | 10 | 14 | 9 | 5 |
分析 (Ⅰ)分类求出函数解析式,即可得出利润y关于需求量n的函数解析式;
(Ⅱ)若利润在区间[500,650]内,日需求量为9、10、11,其对应的频数分别为10、14、9,即可求出概率.
解答 解:(Ⅰ)当日需求量n≥100时,
利润为y=60×10+(n-10)×40=40n+200; …(2分)
当日需求量n<10时,利润为y=60n-(10-n)×70=70n-100.…(4分)
所以利润y关于需求量n的函数解析式为y=$\left\{\begin{array}{l}{40n+200,n≥10,n∈N}\\{70n-100,n<10,n∈N}\end{array}\right.$ …(6分)
(Ⅱ)50天内有4天获得的利润为390元,有8天获得的利润为460元,有10天获得的利润为530元,有14天获得的利润为600元,有9天获得的利润为640元,有5天获得的利润为680元.…(9分)
若利润在区间[500,650]内,日需求量为9、10、11,其对应的频数分别为10、14、9.…(10分)
则利润在区间[500,650]内的概率为$\frac{10+14+9}{50}=\frac{33}{50}$. …(12分)
点评 本题考查分段函数,考查概率的计算,考查学生分析解决问题的能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
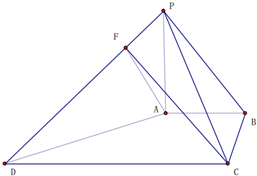 如图,在四棱锥P-ABCD中,已知AB=1,BC=2,CD=4,AB∥CD,BC⊥CD,平面PAB⊥平面ABCD,PA⊥AB,
如图,在四棱锥P-ABCD中,已知AB=1,BC=2,CD=4,AB∥CD,BC⊥CD,平面PAB⊥平面ABCD,PA⊥AB,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com