
 在正方形ABCD中,E为AB的中点,P为以A为圆心,AB为半径的圆弧上的任意一点,设向量$\overrightarrow{AC}=λ\overrightarrow{DE}+μ\overrightarrow{AP}$,当∠PAB=$\frac{π}{3}$时,λ+μ=2,当∠PAB∈[0,$\frac{π}{2}$]时,λ+μ的最小值为$\frac{1}{2}$.
在正方形ABCD中,E为AB的中点,P为以A为圆心,AB为半径的圆弧上的任意一点,设向量$\overrightarrow{AC}=λ\overrightarrow{DE}+μ\overrightarrow{AP}$,当∠PAB=$\frac{π}{3}$时,λ+μ=2,当∠PAB∈[0,$\frac{π}{2}$]时,λ+μ的最小值为$\frac{1}{2}$. 分析 建立坐标系,设正方形ABCD的边长为1,求出向量$\overrightarrow{AC}=λ\overrightarrow{DE}+μ\overrightarrow{AP}$=($\frac{λ}{2}+μcosθ$,-λ+μsinθ )=(1,1),用cosθ,sinθ表示 λ和μ,根据cosθ,sinθ 的取值范围,再结合λ+μ的单调性,求出λ+μ=-1+$\frac{3sinθ+3}{2cosθ+sinθ}$的最小值及当∠PAB=$\frac{π}{3}$时的值.
解答  解:以A为原点,以AB所在的为x轴,
解:以A为原点,以AB所在的为x轴,
如图建立坐标系,设正方形ABCD的边长为1,
则E($\frac{1}{2}$,0),C(1,1),D(0,1),A(0,0).
设 P(cosθ,sinθ),则$\overrightarrow{AC}$=(1,1).
再由向量$\overrightarrow{AC}=λ\overrightarrow{DE}+μ\overrightarrow{AP}$
=λ($\frac{1}{2}$,-1)+μ(cosθ,sinθ)
=($\frac{λ}{2}+μcosθ$,-λ+μsinθ ),
可知$\left\{\begin{array}{l}{\frac{λ}{2}+μcosθ=1}\\{-λ+μsinθ=1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{λ=\frac{2sinθ-2cosθ}{2cosθ+sinθ}}\\{μ=\frac{3}{2cosθ+sinθ}}\end{array}\right.$,
所以λ+μ=$\frac{3+2sinθ-2cosθ}{2cosθ+sinθ}$
=$\frac{(-2cosθ-sinθ)+3sinθ+3}{2cosθ+sinθ}$
=-1+$\frac{3sinθ+3}{2cosθ+sinθ}$.
当∠PAB=$\frac{π}{3}$时,即$θ=\frac{π}{3}$时,
$λ+μ=-1+\frac{3×\frac{\sqrt{3}}{2}+3}{2×\frac{1}{2}+\frac{\sqrt{3}}{2}}$=2;
当∠PAB∈[0,$\frac{π}{2}$]时,即0≤θ≤$\frac{π}{2}$,
所以0≤cosθ≤1,0≤sinθ≤1.
求得(λ+μ)′=$\frac{3cosθ(2cosθ+sinθ)-(3sinθ+3)(-2sinθ+cosθ)}{({2cosθ+sinθ)}^{2}}$
=$\frac{6+6sinθ-3cosθ}{(2cosθ+sinθ)^{2}}$>0,
故λ+μ在[0,$\frac{π}{2}$]上是增函数,
所以当θ=0,即cosθ=1时,这时λ+μ取最小值为$\frac{3+0-2}{2+0}$=$\frac{1}{2}$,
故当∠PAB∈[0,$\frac{π}{2}$]时,λ+μ的最小值为:$\frac{1}{2}$.
点评 本题考查两个向量坐标形式的运算,根据cosθ,sinθ 的取值范围求三角函数式的最值,利用导数研究函数的单调性.用cosθ,sinθ表示 λ和μ 是解题的难点,属于中档题.


科目:高中数学 来源: 题型:解答题
 已知平面直角坐标系中的一个椭圆,它的中心在原点,左焦点为F(-$\sqrt{3}$,0),且抛物线x2=4y的焦点为椭圆的一个顶点,过P(0,2)的直线l分别与椭圆,抛物线交于不同的A,B,C,D四点.
已知平面直角坐标系中的一个椭圆,它的中心在原点,左焦点为F(-$\sqrt{3}$,0),且抛物线x2=4y的焦点为椭圆的一个顶点,过P(0,2)的直线l分别与椭圆,抛物线交于不同的A,B,C,D四点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
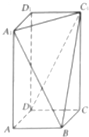 在长方形ABCD-A1B1C1D1中,过A1,C1,B三点的平面截去长方体的一个角后,得到如图所示的几何体,若AB=BC=2,且这个几何体的体积为$\frac{40}{3}$.
在长方形ABCD-A1B1C1D1中,过A1,C1,B三点的平面截去长方体的一个角后,得到如图所示的几何体,若AB=BC=2,且这个几何体的体积为$\frac{40}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com