
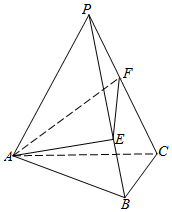
 正三棱锥P-ABC的侧面是底边长为a,顶角为30°的等腰三角形.过点A作这个三棱锥的截面AEF,点E、F分别在棱PB、PC上.
正三棱锥P-ABC的侧面是底边长为a,顶角为30°的等腰三角形.过点A作这个三棱锥的截面AEF,点E、F分别在棱PB、PC上.分析 (1)延长FE,CB,设FE∩BC=D,则AD即为所求直线;
(2)作出三棱锥的侧面展开图,则AA′为最短距离,利用余弦定理求出PA,则AA′=$\sqrt{2}PA$.
解答 解:(1)延长FE,CB,设FE∩BC=D
连结AD,则直线AD为平面AEF与平面ABC的交线.
(2)作三棱锥P-ABC的侧面展开图,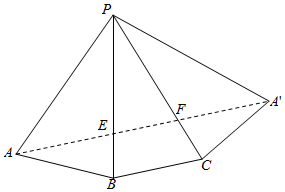
连结AA′,则△AEF的周长最小值为AA′.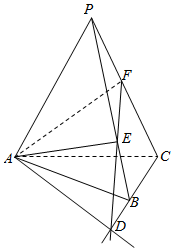
由题意可知PA=PB,AB=a,∠APB=30°,
由余弦定理得:cos30°=$\frac{2P{A}^{2}-{a}^{2}}{2P{A}^{2}}$=$\frac{\sqrt{3}}{2}$,解得PA=$\sqrt{2+\sqrt{3}}$a.
∴AA′=$\sqrt{2}PA$=$\sqrt{4+2\sqrt{3}}$a=($\sqrt{3}+1$)a.
此时,EF∥BC,故BC∥平面AEF.
点评 本题考查了空间直线与平面的位置关系,多面体表面的最短距离问题,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{7}-\frac{y^2}{3}=1$ | B. | $\frac{y^2}{3}-\frac{x^3}{7}=1$ | C. | $\frac{x^2}{3}-{y^2}=1$ | D. | ${y^2}-\frac{x^2}{3}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=log0.5(x+1) | B. | $y={log_2}\sqrt{{x^2}-1}$ | ||
| C. | $y={log_2}\frac{1}{x}$ | D. | $y={log_{\frac{1}{2}}}(5-4x+{x^2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
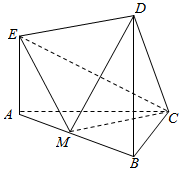 如图所示的几何体中,EA⊥平面ABC,BD⊥平面ABC,AC=BC=BD=2AE=$\frac{{\sqrt{2}}}{2}AB$,M是AB的中点.
如图所示的几何体中,EA⊥平面ABC,BD⊥平面ABC,AC=BC=BD=2AE=$\frac{{\sqrt{2}}}{2}AB$,M是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com