
分析 (1)根据1的替换,结合基本不等式的应用求出函数f(x)的最小值即可得到结论.
(2)根据绝对值的应用将不等式进行表示为分段函数形式,进行求解即可.
解答 解:(1)f(x)=$\frac{1}{9si{n}^{2}x}$+$\frac{4}{9co{s}^{2}x}$=($\frac{1}{9si{n}^{2}x}$+$\frac{4}{9co{s}^{2}x}$)(sin2x+cos2x)
=$\frac{1}{9}$(5+$\frac{4sin^2x}{cos^2x}$+$\frac{cos^2x}{sin^2x}$)≥$\frac{1}{9}$(5+2$\sqrt{\frac{4sin^2x}{cos^2x}•\frac{cos^2x}{sin^2x}}$)=$\frac{1}{9}$(5+2$\sqrt{4}$)=$\frac{1}{9}$(5+4)=1,
当且仅当$\frac{4sin^2x}{cos^2x}$=$\frac{cos^2x}{sin^2x}$,即$tanx=\frac{{\sqrt{2}}}{2}$时等号成立,
若f(x)≥t恒成立,
∴t≤1,即t的最大值为1.
(2)由题$\left|{x+1}\right|+\left|{x-2}\right|=\left\{\begin{array}{l}1-2x,x<-1\\ 3,-1≤x≤2\\ 2x-1,x>2\end{array}\right.$,--------(5分)
则由|x+1|+|x-2|≥5得,
当x<-1,得1-2x≥5得2x≤-4,即x≤-2,此时x≤-2,
当-1≤x≤2得3≥5,此时不等式不成立,
当x>2时,得2x-1≥5,即x≥3,
综上x≤-2或x≥3,
不等式的解集为(-∞,-2]∪[3,+∞)------(10分)
点评 本题主要考查不等式恒成立以及绝对值不等式的求解,根据基本不等式的解法利用1的代换进行求解是解决本题的关键.综合考查绝对值不等式的解法.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | x<-$\frac{3}{8}$ | B. | x<-$\frac{1}{2}$ | C. | x≤-$\frac{1}{2}$ | D. | x≤-$\frac{3}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
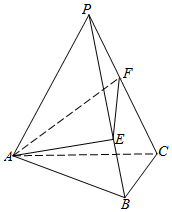 正三棱锥P-ABC的侧面是底边长为a,顶角为30°的等腰三角形.过点A作这个三棱锥的截面AEF,点E、F分别在棱PB、PC上.
正三棱锥P-ABC的侧面是底边长为a,顶角为30°的等腰三角形.过点A作这个三棱锥的截面AEF,点E、F分别在棱PB、PC上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com