
有三张正面分别写有数字—2,—1,1的卡片,它们的背面完全相同,将这三张卡片背面朝上洗匀后随机抽取一张,以其正面的数字作为x的值。放回卡片洗匀,再从三张卡片中随机抽取一张,以其正面的数字作为y的值,两次结果记为(x,y)。
(1)用树状图或列表法表示(x,y)所有可能出现的结果;
(2)求使分式 有意义的(x,y)出现的概率;
有意义的(x,y)出现的概率;
(3)化简分式 ;并求使分式的值为整数的(x,y)出现的概率。
;并求使分式的值为整数的(x,y)出现的概率。
(1) 共有(—2,—2),(—2,—1),(—2,1),(—1,—2),(—1,—1),(—1,1),(1,—2),(1,—1),(1,1)9种可能出现的结果
(2)
(3)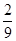
解析试题分析:解:(1)树状图如下: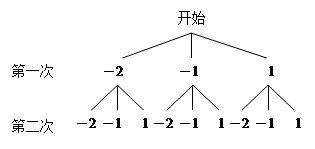
共有(—2,—2),(—2,—1),(—2,1),(—1,—2),(—1,—1),(—1,1),(1,—2),(1,—1),(1,1)9种可能出现的结果。 3分
(2)要使分式有意义,必须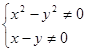 ,即
,即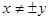 ,
,
符合条件的有(—2,—1),(—2,1),(—1,—2),(1,—2)四种结果,
∴ 使分式 有意义的(x,y)出现的概率为
有意义的(x,y)出现的概率为 。 6分
。 6分
(3)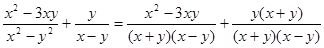
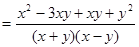
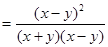
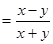
能使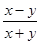 的值为整数的有(—2,1),(1,—2)两种结果,其概率为
的值为整数的有(—2,1),(1,—2)两种结果,其概率为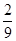 。 …9分
。 …9分
考点:随机事件的概率
点评:解决关键是利用代数式的化简求值找到满足题意的事件数,来求解概率,属于基础题。


科目:高中数学 来源: 题型:解答题
若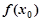 是函数
是函数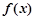 在点
在点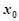 附近的某个局部范围内的最大(小)值,则称
附近的某个局部范围内的最大(小)值,则称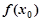 是函数
是函数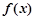 的一个极值,
的一个极值,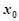 为极值点.已知
为极值点.已知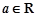 ,函数
,函数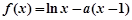 .
.
(Ⅰ)若 ,求函数
,求函数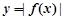 的极值点;
的极值点;
(Ⅱ)若不等式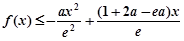 恒成立,求
恒成立,求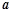 的取值范围.
的取值范围.
(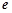 为自然对数的底数)
为自然对数的底数)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数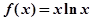 ,
,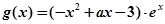 (其中
(其中 实数,
实数,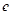 是自然对数的底数).
是自然对数的底数).
(Ⅰ)当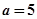 时,求函数
时,求函数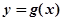 在点
在点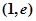 处的切线方程;
处的切线方程;
(Ⅱ)求 在区间
在区间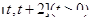 上的最小值;
上的最小值;
(Ⅲ) 若存在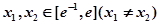 ,使方程
,使方程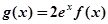 成立,求实数
成立,求实数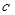 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知定义域为[0,1]的函数同时满足以下三个条件:①对任意 ,总有
,总有 ;②
;② ;③若
;③若 ,则有
,则有 成立.
成立.
(1) 求 的值;(2) 函数
的值;(2) 函数 在区间[0,1]上是否同时适合①②③?并予以证明
在区间[0,1]上是否同时适合①②③?并予以证明
(3) 假定存在 ,使得
,使得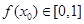 ,且
,且 ,求证:
,求证: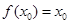
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数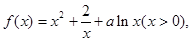
(1)若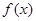 在
在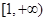 上单调递增,求
上单调递增,求 的取值范围;
的取值范围;
(2)若定义在区间D上的函数 对于区间
对于区间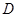 上的任意两个值
上的任意两个值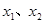 总有以下不等式
总有以下不等式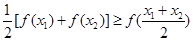 成立,则称函数
成立,则称函数 为区间
为区间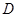 上的 “凹函数”.试证当
上的 “凹函数”.试证当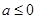 时,
时,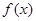 为“凹函数”.
为“凹函数”.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
已知函数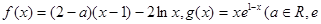 为自然对数的底数).
为自然对数的底数).
当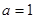 时,求
时,求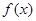 的单调区间;若函数
的单调区间;若函数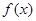 在
在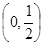 上无零点,求
上无零点,求 最小值;
最小值;
若对任意给定的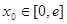 ,在
,在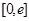 上总存在两个不同的
上总存在两个不同的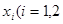 ),使
),使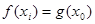 成立,求
成立,求 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com