
已知定义域为[0,1]的函数同时满足以下三个条件:①对任意 ,总有
,总有 ;②
;② ;③若
;③若 ,则有
,则有 成立.
成立.
(1) 求 的值;(2) 函数
的值;(2) 函数 在区间[0,1]上是否同时适合①②③?并予以证明
在区间[0,1]上是否同时适合①②③?并予以证明
(3) 假定存在 ,使得
,使得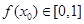 ,且
,且 ,求证:
,求证: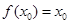
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
有三张正面分别写有数字—2,—1,1的卡片,它们的背面完全相同,将这三张卡片背面朝上洗匀后随机抽取一张,以其正面的数字作为x的值。放回卡片洗匀,再从三张卡片中随机抽取一张,以其正面的数字作为y的值,两次结果记为(x,y)。
(1)用树状图或列表法表示(x,y)所有可能出现的结果;
(2)求使分式 有意义的(x,y)出现的概率;
有意义的(x,y)出现的概率;
(3)化简分式 ;并求使分式的值为整数的(x,y)出现的概率。
;并求使分式的值为整数的(x,y)出现的概率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com