
证明函数f(x)=x+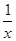 在(0,1)上是减函数.
在(0,1)上是减函数.
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:高中数学 来源: 题型:解答题
已知 ,函数
,函数
(1)求 的极小值;
的极小值;
(2)若 在
在 上为单调增函数,求
上为单调增函数,求 的取值范围;
的取值范围;
(3)设 ,若在
,若在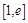 (
( 是自然对数的底数)上至少存在一个
是自然对数的底数)上至少存在一个 ,使得
,使得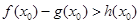 成立,求
成立,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 (a>0,且a≠1),
(a>0,且a≠1), =
= .
.
(1)函数 的图象恒过定点A,求A点坐标;
的图象恒过定点A,求A点坐标;
(2)若函数 的图像过点(2,
的图像过点(2, ),证明:函数
),证明:函数 在
在 (1,2)上有唯一的零点.
(1,2)上有唯一的零点.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知定义域为[0,1]的函数同时满足以下三个条件:①对任意 ,总有
,总有 ;②
;② ;③若
;③若 ,则有
,则有 成立.
成立.
(1) 求 的值;(2) 函数
的值;(2) 函数 在区间[0,1]上是否同时适合①②③?并予以证明
在区间[0,1]上是否同时适合①②③?并予以证明
(3) 假定存在 ,使得
,使得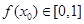 ,且
,且 ,求证:
,求证: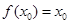
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分15分)
已知函数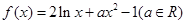
(Ⅰ)求函数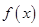 的单调区间;
的单调区间;
(Ⅱ)若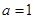 ,试分别解答以下两小题.
,试分别解答以下两小题.
(ⅰ)若不等式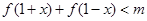 对任意的
对任意的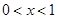 恒成立,求实数
恒成立,求实数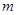 的取值范围;
的取值范围;
(ⅱ)若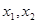 是两个不相等的正数,且
是两个不相等的正数,且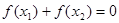 ,求证:
,求证: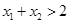 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分10分)
已知函数f(x)=|x-a|.
(1)若不等式f(x)≤3的解集为{x|-1≤x≤5},求实数a的值;
(2)在(1)的条件下,若f(x)+f(x+5)≥m对一切实数x恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数
 ,且
,且 能表示成一个奇函数
能表示成一个奇函数 和一个偶函数
和一个偶函数 的和.
的和.
(1)求 和
和 的解析式.
的解析式.
(2)命题 :函数
:函数 在区间
在区间 上是增函数;命题
上是增函数;命题 :函数
:函数 是减函数,如果命题
是减函数,如果命题 、
、 有且仅有一个是真命题,求实数
有且仅有一个是真命题,求实数 的取值范围.
的取值范围.
(3)在(2)的条件下,比较 和
和 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com