
【题目】如图,四棱锥P﹣ABCD的侧面PAD是正三角形,底面ABCD为菱形,A点E为AD的中点,若BE=PE. 
(1)求证:PB⊥BC;
(2)若∠PEB=120°,求二面角A﹣PB﹣C的余弦值.
【答案】
(1)证明:由BE=PE,AB=PA,AE=AE,得△AEP≌△AEB,
∴∠EAB=60°,且AD⊥BE,
又∵AD⊥PE,
∴AD⊥平面PBE,
∵PB平面PBE,得AD⊥PB,
又AD∥BC,
∴PB⊥BC.
(2)解:如图,过P作PO⊥平面ABCD,交BE延长线于O,
以O为坐标原点,过O作DA的平行线为x轴,OB为y轴,OP为z轴,建立空间直角坐标系,
P(0,0, ![]() ),B(0,
),B(0, ![]() ,0),PB的中占点G(0,
,0),PB的中占点G(0, ![]() ,
, ![]() ),连结AG,
),连结AG,
又A(1, ![]() ,0),C(﹣2,
,0),C(﹣2, ![]() ,0),由此得到
,0),由此得到 ![]() =(1,﹣
=(1,﹣ ![]() ,﹣
,﹣ ![]() ),
),
![]() =(0,
=(0, ![]() ),
), ![]() =(﹣2,0,0),
=(﹣2,0,0),
∴ ![]() =0,
=0, ![]() =0,
=0,
∴ ![]() ,
, ![]() ,
,
∵ ![]() 的夹角为θ等于所求二面角二面角A﹣PB﹣C的平面角,
的夹角为θ等于所求二面角二面角A﹣PB﹣C的平面角,
∴cos ![]() =
=  =﹣
=﹣ ![]() .
.
∴二面角A﹣PB﹣C的余弦值为﹣ ![]() .
.
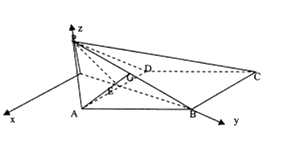
【解析】(1)推导出∠EAB=60°,且AD⊥BE,AD⊥PE,从而AD⊥平面PBE,进而AD⊥PB,由此能证明PB⊥BC.(2)过P作PO⊥平面ABCD,交BE延长线于O,以O为坐标原点,过O作DA的平行线为x轴,OB为y轴,OP为z轴,建立空间直角坐标系,利用向量法能求出二面角二面角A﹣PB﹣C的余弦值.
【考点精析】掌握空间中直线与直线之间的位置关系是解答本题的根本,需要知道相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点.


科目:高中数学 来源: 题型:
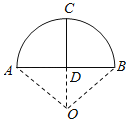
【题目】《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章给出计算弧田面积所用的经验方式为:弧田面积=![]() (弦×矢+矢2),弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角为
(弦×矢+矢2),弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角为![]() ,半径等于
,半径等于![]() 米的弧田,按照上述经验公式计算所得弧田面积约是
米的弧田,按照上述经验公式计算所得弧田面积约是 ![]()
A. ![]() 平方米 B.
平方米 B. ![]() 平方米
平方米
C. ![]() 平方米 D.
平方米 D. ![]() 平方米
平方米
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在△ABC和△ACD中,∠ACB=∠ADC=90°,∠BAC=∠CAD,⊙O是以AB为直径的圆,DC的延长线与AB的延长线交于点E.
(Ⅰ)求证:DC是⊙O的切线;
(Ⅱ)若EB=6,EC=6 ![]() ,求BC的长.
,求BC的长.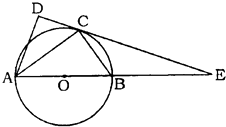
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆N的标准方程为(x-5)2+(y-6)2=a2(a>0).
(1)若点M(6,9)在圆上,求a的值;
(2)已知点P(3,3)和点Q(5,3),线段PQ(不含端点)与圆N有且只有一个公共点,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:y=﹣x+1与椭圆C: ![]() =1(a>b>0))相交于不同的两点A、B,且线段AB的中点P的坐标为(
=1(a>b>0))相交于不同的两点A、B,且线段AB的中点P的坐标为( ![]() ,
, ![]() )
) 
(1)求椭圆C离心率;
(2)设O为坐标原点,且2|OP|=|AB|,求椭圆C的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设A={x|2x2+ax+2=0},B={x|x2+3x+2a=0},A∩B={2}.
(1)求a的值及集合A、B;
(2)设集合U=A∪B,求(CuA)∪(CuB)的所有子集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() :
: ![]() (
(![]() )的离心率为
)的离心率为![]() ,连接椭圆
,连接椭圆![]() 的四个顶点所形成的四边形面积为
的四个顶点所形成的四边形面积为![]() .
.

(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若椭圆![]() 上点
上点![]() 到定点
到定点![]() (
(![]() )的距离的最小值为1,求
)的距离的最小值为1,求![]() 的值及点
的值及点![]() 的坐标;
的坐标;
(3)如图,过椭圆![]() 的下顶点作两条互相垂直的直线,分别交椭圆
的下顶点作两条互相垂直的直线,分别交椭圆![]() 于点
于点![]() ,
, ![]() ,设直线
,设直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() :
: ![]() 分别与直线
分别与直线![]() ,
, ![]() 交于点
交于点![]() ,
, ![]() .记
.记![]() ,
, ![]() 的面积分别为
的面积分别为![]() ,
, ![]() ,是否存在直线
,是否存在直线![]() ,使得
,使得![]() ?若存在,求出所有直线
?若存在,求出所有直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)的图象过点(0,4),对任意x满足f(3﹣x)=f(x),且f(1)=2.
(1)若f(x)在(a,2a﹣1)上单调递减,求实数a的取值范围.
(2)设函数h(x)=f(x)﹣(2t﹣3)x,其中t∈R,求h(x)在区间[0,1]上的最小值g (t).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com