
| A. | 直角三角形 | B. | 等腰直角三角形 | C. | 正三角形 | D. | 钝角三角形 |
分析 根据题意画出图形,结合图形,利用平面向量的线性表示与数量积运算,得出边长b=c,即可得出△ABC是正三角形.
解答 解:如图所示,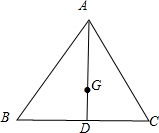
△ABC中,设D是BC的中点,且$\overrightarrow{AB}$=$\overrightarrow{c}$,$\overrightarrow{AC}$=$\overrightarrow{b}$;
由条件得$\overrightarrow{c}$•$\overrightarrow{b}$=$\overrightarrow{AB}$•$\overrightarrow{AC}$=bc•cos$\frac{π}{3}$=6,
∴bc=12;
又$\overrightarrow{AG}$=$\frac{2}{3}$$\overrightarrow{AD}$=$\frac{1}{3}$($\overrightarrow{c}$+$\overrightarrow{b}$),且|$\overrightarrow{AG}$|=2,
∴${(\overrightarrow{c}+\overrightarrow{b})}^{2}$=36,
即c2+b2+2$\overrightarrow{c}$•$\overrightarrow{b}$=36,
∴c2+b2-24=0,
∴c2-2bc+b2=0,
即(b-c)2=0,
∴b=c,
∴△ABC是正三角形.
故选:C.
点评 本题考查了平面向量的线性表示与数量积运算问题,也考查了数形结合的解题方法,是综合性题目.


科目:高中数学 来源: 题型:选择题
| A. | x0<a | B. | x0>a | C. | x0<c | D. | x0>c |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 概率是频率的稳定值,频率是概率的近似值 | |
| B. | 已知事件M⊆N,则当M发生时,N一定发生 | |
| C. | 若A,B为互斥事件,则P(A)+P(B)<1 | |
| D. | 若一生产厂家称,我们厂生产的产品合格率是0.98,则任取一件该产品,其是合格品的可能性大小为98% |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com