
分析 利用幂函数、指数函数、对数函数及绝对值函数的性质对①②③④逐个判断即可.
解答 解:①y=x${\;}^{\frac{1}{2}}$在(0,1)单调递增函数,
②y=21-x=2×($\frac{1}{2}$)x,单调递减函数,
③y=ln(x+1)单调递增函数,
④y=|1-x|=$\left\{\begin{array}{l}{-x+1,x≤1}\\{x-1,x>1}\end{array}\right.$,故在(0,1)上单调递减函数,
故综上所述,②④为(0,1)上的减函数.
故答案为:②④
点评 本题考查基本初等函数的单调性,熟练掌握其图象性质是解决问题的关键,属于基础题.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源: 题型:解答题
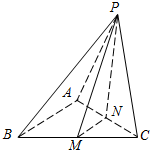 如图,在三棱锥P-ABC中,PA=PC,BC=4,AC=2.M为BC的中点,N为AC上一点,且MN∥平面PAB,MN=$\sqrt{3}$.求证:
如图,在三棱锥P-ABC中,PA=PC,BC=4,AC=2.M为BC的中点,N为AC上一点,且MN∥平面PAB,MN=$\sqrt{3}$.求证:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{10}{9}$ | B. | 4 | C. | $\frac{40}{9}$ | D. | $\frac{56}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
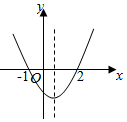 函数f(x)=$\frac{1}{3}$x3+ax2+bx+c(a,b,c∈R)的导函数的图象如图所示:
函数f(x)=$\frac{1}{3}$x3+ax2+bx+c(a,b,c∈R)的导函数的图象如图所示:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)与g(x)的最大值不同 | |
| B. | 函数f(x)与g(x)在$(\frac{3π}{4},\;\;\frac{5π}{4})$上都为增函数 | |
| C. | 函数f(x)与g(x)的图象的对称轴相同 | |
| D. | 将函数f(x)的图象上各点的横坐标缩短为原来的$\frac{1}{2}$,纵坐标不变,再通过平移能得到g(x)的图象 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
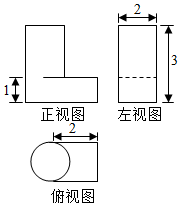 一个空间几何体的三视图如图所示,则该几何体的体积为( )
一个空间几何体的三视图如图所示,则该几何体的体积为( )| A. | 4+3π | B. | 4+4π | C. | 4-$\frac{3π}{2}$ | D. | 4+$\frac{5π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
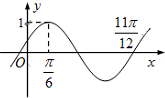 函数f(x)=Asin(wx+φ)(A>0,w>0,φ∈R)的部分图象如图所示,则将y=f(x)的图象向右平移π6个单位后得到g(x),得到的函数图象对称轴为x=$\frac{kπ}{2}$+$\frac{π}{3}$,k∈Z,函数g(x)的解析式为y=sin(2x-$\frac{π}{6}$).
函数f(x)=Asin(wx+φ)(A>0,w>0,φ∈R)的部分图象如图所示,则将y=f(x)的图象向右平移π6个单位后得到g(x),得到的函数图象对称轴为x=$\frac{kπ}{2}$+$\frac{π}{3}$,k∈Z,函数g(x)的解析式为y=sin(2x-$\frac{π}{6}$).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com