练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    函数f(x)＝ax＋b的零点是－1(a≠0)，则函数g(x)＝ax2＋bx的零点是(　　)

    A．－1                               B．0

    C．－1和0                           D．1和0


    C

    [解析]　由条件知f(－1)＝0，∴b＝a，∴g(x)＝ax2＋bx＝ax(x＋1)的零点为0和－1.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    在正方体ABCD－A1B1C1D1内随机取点则该点落在三棱锥A1－ABC内的概率是(　　)

    A．                                B．

    C．                                D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)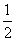＝()ax，a为常数，且函数的图象过点(－1,2)．

    (1)求a的值；

    (2)若g(x)＝4－x－2，且g(x)＝f(x)，求满足条件的x的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)，g(x)分别由下表给出

     

    x

    1

    2

    3

    f(x)

    2

    3

    1

    　　

    x

    1

    2

    3

    g(x)

    3

    2

    1

    则f[g(1)]的值为________；

    当g[f(x)]＝2时，x＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝x＋x3，x∈R.

    (1)判断函数f(x)的单调性，并证明你的结论；

    (2)若a，b∈R，且a＋b>0，试比较f(a)＋f(b)与0的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若函数f(x)＝x3－x－1在区间[1,1.5]内的一个零点附近函数值用二分法逐次计算列表如下

    x

    1

    1.5

    1.25

    1.375

    1.3125

    f(x)

    －1

    0.875

    －0.2969

    0.2246

    －0.05151

    那么方程x3－x－1＝0的一个近似根(精确度为0,1)为(　　)

    A．1.2                               B．1.3125

    C．1.4375                            D．1.25

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    求函数f(x)＝2x＋lg(x＋1)－2的零点个数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设a＝log32，b＝ln2，c＝5－，则a，b，c大小关系为______．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知sinα·cosα<0，sinαtanα>0，化简

    ＝________.

    查看答案和解析>>

    同步练习册答案