
分析 利用复数代数形式的乘除运算化简z,求出$\overline{z}$,进一步得到$\overline z•i$在复平面内对应的点的坐标得答案.
解答 解:∵$z=\frac{1}{1+i}$=$\frac{1-i}{(1+i)(1-i)}=\frac{1}{2}-\frac{i}{2}$,
∴$\overline z•i$=$(\frac{1}{2}+\frac{i}{2})•i=-\frac{1}{2}+\frac{i}{2}$,
则$\overline z•i$在复平面内对应的点的坐标为($-\frac{1}{2},\frac{1}{2}$),位于第二象限.
故答案为:二.
点评 本题考查复数代数形式的乘除运算,考查复数的代数表示法及其几何意义,是基础题.


 优生乐园系列答案
优生乐园系列答案科目:高中数学 来源: 题型:选择题
| A. | f (1)>c>f (-1) | B. | f (1)<c<f (-1) | C. | c>f (-1)>f (1) | D. | c<f (-1)<f (1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{4}{5}$ | B. | $\frac{4}{5}$ | C. | ±$\frac{4}{5}$ | D. | ±$\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (10,+∞) | B. | (-∞,0)∪(11,+∞) | C. | (-∞,11) | D. | (-∞,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
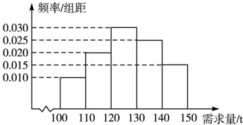 经销商经销某种农产品,在一个销售季度内,每售出1t该产品获利润500元,未售出的产品,每1t亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了130t该农产品.以X(单位:t,100≤X≤150)表示下一个销售季度内的市场需求量,T(单位:元)表示下一个销售季度内经销该农产品的利润.
经销商经销某种农产品,在一个销售季度内,每售出1t该产品获利润500元,未售出的产品,每1t亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了130t该农产品.以X(单位:t,100≤X≤150)表示下一个销售季度内的市场需求量,T(单位:元)表示下一个销售季度内经销该农产品的利润.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com