
| OA |
| a |
| OB |
| b |
| OC |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| a |
| b |
| OP |
| a |
| b |
| c |
| ||
| 3 |
| c |
| a |
| b |
| c |
| a |
| c |
| b |
| c |
| a |
| b |
| π |
| 2 |
| c |
| a |
| b |
| a |
| b |
| ||
| 3 |
| ||
| 2 |
| ||
| 6 |
| c |
| a |
| b |
| c |
| a |
| c |
| b |
| c |
| a |
| b |
| π |
| 2 |
| c |
| a |
| b |
| π |
| 2 |
| c |
| a |
| b |
| a |
| b |
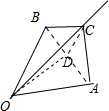 又BC=AC,D为AB的中点,则CD⊥AB,∴OD⊥CD,又OD=DA=
又BC=AC,D为AB的中点,则CD⊥AB,∴OD⊥CD,又OD=DA=
| ||
| 2 |
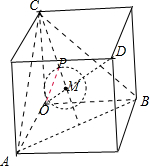 补全正方体,对角线OD与平面ABC相交于点M,点M为等边三角形的中心,OM=
补全正方体,对角线OD与平面ABC相交于点M,点M为等边三角形的中心,OM=| 1 |
| 3 |
| ||
| 3 |
| OP |
| a |
| b |
| c |
| OD |
| ||
| 3 |
| OM | ||||
|
| ||
| 2 |
| OP2-OM2 |
| ||
| 6 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
 如图,四面体ABCD中,平面ABC⊥平面BCD,AC=AB,CB=CD,∠DCB=120°,点E在BD上,且CE=DE.
如图,四面体ABCD中,平面ABC⊥平面BCD,AC=AB,CB=CD,∠DCB=120°,点E在BD上,且CE=DE.查看答案和解析>>
科目:高中数学 来源: 题型:
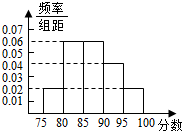 某市教育局为了了解高三学生体育达标情况,在某学校的高三学生体育达标成绩中随机抽取50个进行调研,按成绩分组:第l组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示:若要在成绩较高的第3,4,5组中用分层抽样抽取6名学生进行复查:
某市教育局为了了解高三学生体育达标情况,在某学校的高三学生体育达标成绩中随机抽取50个进行调研,按成绩分组:第l组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示:若要在成绩较高的第3,4,5组中用分层抽样抽取6名学生进行复查:查看答案和解析>>
科目:高中数学 来源: 题型:
| 5 |
| 3 |
| 5 |
| 9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com