
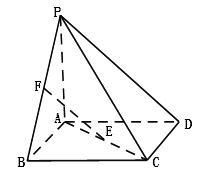
【题目】如图,四棱锥 ![]() 的底面
的底面 ![]() 为正方形,
为正方形, ![]() ⊥底面
⊥底面 ![]() ,
, ![]() 分别是
分别是 ![]() 的中点,
的中点, ![]() .
.
(Ⅰ)求证 ![]() ∥平面
∥平面 ![]() ;
;
(Ⅱ)求直线 ![]() 与平面
与平面 ![]() 所成的角;
所成的角;
(Ⅲ)求四棱锥 ![]() 的外接球的体积.
的外接球的体积.
【答案】解:(Ⅰ)如图,连结 ![]() ,则
,则 ![]() 是
是 ![]() 的中点,又
的中点,又 ![]() 是
是 ![]() 的中点,
的中点,
∴ ![]() .又∵
.又∵ ![]() 平面
平面 ![]() ,
, ![]() 面
面 ![]()
∴ ![]() 平面
平面 ![]() .
.
(Ⅱ)取 ![]() 的中点
的中点 ![]() ,连接
,连接 ![]() .
.
在正方形 ![]() 中,
中, ![]() 是
是 ![]() 的中点,有
的中点,有 ![]() .
.
∵ ![]() 平面
平面 ![]() ,
, ![]() 平面
平面 ![]() ,∴
,∴ ![]() ,
,
∵ ![]() ,∴
,∴ ![]() 平面
平面 ![]() ,
,
∴ ![]() 是直线
是直线 ![]() 在平面
在平面 ![]() 的射影,∴
的射影,∴ ![]() 是直线
是直线 ![]() 与平面
与平面 ![]() 所成的角,
所成的角,
在直角三角形 ![]() 中,
中, ![]() ,所以
,所以 ![]() .
.
∴直线 ![]() 与平面
与平面 ![]() 所成的角为45°.
所成的角为45°.
(Ⅲ)设四棱锥 ![]() 的外接球半径为
的外接球半径为 ![]() ,
, ![]() ,则
,则
![]() ,即
,即 ![]() .
.
所以外接球的体积为 ![]() ..
..
【解析】(1)根据题意作出辅助线,利用线面平行的判定定理即可得证。(2)由题意结合线面垂直的判断定理可得证H E ⊥ 平面 P A B,进而找出二面角的平面角结合题中已知在直角三角形中求出线面角即可。(3)根据题意把四棱锥补成为一个球内接长方体,球的直径为长方体的体对角线进而求出半径再结合球的体积公式代入数值求出即可。
【考点精析】本题主要考查了直线与平面平行的性质和直线与平面垂直的判定的相关知识点,需要掌握一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行;简记为:线面平行则线线平行;一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,若a2+c2+ ![]() ac=b2 , sinA=
ac=b2 , sinA= ![]() .
.
(1)求sinC的值;
(2)若a=2,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设区间D=[﹣3,3],定义在D上的函数f(x)=ax3+bx+1(a>0,b∈R),集合A={a|x∈D,f(x)≥0}.
(1)若b= ![]() ,求集合A;
,求集合A;
(2)设常数b<0 ①讨论f(x)的单调性;
②若b<﹣1,求证:A=.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某淘宝商城在2017年前7个月的销售额![]() (单位:万元)的数据如下表,已知
(单位:万元)的数据如下表,已知![]() 与
与![]() 具有较好的线性关系.
具有较好的线性关系. 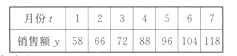
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)分析该淘宝商城2017年前7个月的销售额的变化情况,并预测该商城8月份的销售额.
附:回归直线的斜率和截距的最小二乘估计公式分别为:
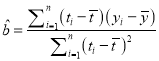 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设 ![]() 是两个平面,
是两个平面, ![]() 是两条直线,有下列四个命题:
是两条直线,有下列四个命题:
⑴如果 ![]() ,那么
,那么 ![]() .
.
⑵如果 ![]() ,那么
,那么 ![]() .
.
⑶如果 ![]() ,那么
,那么 ![]() .
.
其中正确命题的个数是( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合M={x||x|<1},N={y|y=2x , x∈M},则集合R(M∩N)等于( )
A.(﹣∞, ![]() ]
]
B.( ![]() ,1)
,1)
C.(﹣∞, ![]() ]∪[1,+∞)
]∪[1,+∞)
D.[1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的奇函数f(x),当x≥0时,f(x)= ![]() ,则关于x的函数F(x)=f(x)﹣a(0<a<1)的所有零点之和为( )
,则关于x的函数F(x)=f(x)﹣a(0<a<1)的所有零点之和为( )
A.3a﹣1
B.1﹣3a
C.3﹣a﹣1
D.1﹣3﹣a
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 上的一个最高点的坐标为
上的一个最高点的坐标为![]() ,由此点到相邻最低点间的曲线与x轴交于点
,由此点到相邻最低点间的曲线与x轴交于点![]() ,若
,若![]() .
.
(1)求![]() 的解析式.
的解析式.
(2)求![]() 在
在![]() 上的值域.
上的值域.
(3)若对任意实数![]() ,不等式
,不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com