
【题目】已知集合A={x|3≤3x≤27},B={x|log2x>1}. (Ⅰ)求A∩B,A∪B;
(Ⅱ)已知非空集合C={x|1<x≤a},若CA,求实数a的取值范围.
【答案】解:(Ⅰ)集合A={x|3≤3x≤27}={x|1≤x≤3} B={x|log2x>1}={x|x>2}
∴A∩B={x|2<x≤3}
A∪B={x|x≥1}.
(Ⅱ)∵非空集合C={x|1<x≤a},∴a>1,
又CA={x|1≤x≤3},所以a≤3.
综上得a的取值范围是1<a≤3.
【解析】(Ⅰ)先分别求出集合A,B,由此能求出A∩B,A∪B.(Ⅱ)由非空集合C={x|1<x≤a},得a>1,再由CA={x|1≤x≤3},能求出a的取值范围.
【考点精析】掌握集合的并集运算和集合的交集运算是解答本题的根本,需要知道并集的性质:(1)A![]() A∪B,B
A∪B,B![]() A∪B,A∪A=A,A∪
A∪B,A∪A=A,A∪![]() =A,A∪B=B∪A;(2)若A∪B=B,则A
=A,A∪B=B∪A;(2)若A∪B=B,则A![]() B,反之也成立;交集的性质:(1)A∩B
B,反之也成立;交集的性质:(1)A∩B![]() A,A∩B
A,A∩B![]() B,A∩A=A,A∩
B,A∩A=A,A∩![]() =
=![]() ,A∩B=B∩A;(2)若A∩B=A,则A
,A∩B=B∩A;(2)若A∩B=A,则A![]() B,反之也成立.
B,反之也成立.


科目:高中数学 来源: 题型:
【题目】习大大构建的“一带一路”经济带的发展规划已经得到了越来越多相关国家的重视和参与.岳阳市旅游局顺潮流、乘东风,闻讯而动,决定利用旅游资源优势,撸起袖子大干一场.为了了解游客的情况,以便制定相应的策略.在某月中随机抽取甲、乙两个景点各10天的游客数,画出茎叶图如下:
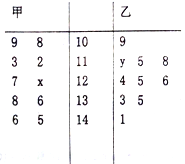
(1)若景点甲中的数据的中位数是125,景点乙中的数据的平均数是124,求![]() 的值;
的值;
(2)若将图中景点甲中的数据作为该景点较长一段时期内的样本数据.今从这段时期内任取4天,记其中游客数超过120人的天数为![]() ,求概率
,求概率![]() ;
;
(3)现从上图的共20天的数据中任取2天的数据(甲、乙两景点中各取1天),记其中游客数不低于115且不高于125人的天数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,过抛物线y2=2px(p>0)焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=2|BF|,且|AF|=3,则此抛物线的方程为( ) 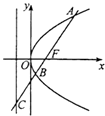
A.y2=3x
B.y2=9x
C.y2= ![]() x
x
D.y2= ![]() x
x
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a∈R,设命题p:指数函数y=ax(a>0且a≠1)在R上单调递增;命题q:函数y=ln(ax2﹣ax+1)的定义域为R,若“p且q”为假,“p或q”为真,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)的对称轴x=﹣2,f(x)的图象被x轴截得的弦长为2 ![]() ,且满足f(0)=1.
,且满足f(0)=1.
(1)求f(x)的解析式;
(2)若f(( ![]() )x)>k,对x∈[﹣1,1]恒成立,求实数k的取值范围.
)x)>k,对x∈[﹣1,1]恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆O:x2+y2=4与x轴负半轴的交点为A,点P在直线l: ![]() x+y﹣a=0上,过点P作圆O的切线,切点为T.
x+y﹣a=0上,过点P作圆O的切线,切点为T.
(1)若a=8,切点T( ![]() ,﹣1),求直线AP的方程;
,﹣1),求直线AP的方程;
(2)若PA=2PT,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c,已知A= ![]() ,b2﹣a2=
,b2﹣a2= ![]() c2 .
c2 .
(1)求tanC的值;
(2)若△ABC的面积为3,求b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com