练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    15．如图，已知F1，F2是双曲线$C：\frac{x^2}{2}-\frac{y^2}{2}=1$的左，右焦点，点A在双曲线的右支上，线段AF1与双曲线左支相交于点B，△F2AB的内切圆与BF2相切于点E，若|AF2|=2|BF1|，则|BE|=$2\sqrt{2}$．

    分析 设|BF1|=m，则|AF2|=2m，由双曲线的定义可得|AF1|=2a+2m，|BF2|=m+2a，|EF2|=m+2a-|BE|，再由内切圆的性质，求得a解得|BE|=2a=2$\sqrt{2}$．

    解答 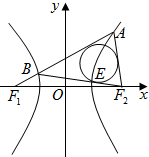解：设|BF1|=m，则|AF2|=2m，
    由双曲线的定义有|AF1|=|AF2|+2a=2a+2m，
    |BF2|=m+2a，|EF2|=m+2a-|BE|
    ∵|AB|=|AF2|-|EF2|+|BE|=2m-（m+2a-|BE|）+|BE|
    ∴|AF1|=∵|AB|+|BF1|
    即有2a+2m=2m-（m+2a-|BE|）+|BE|+m，
    解得|BE|=2a=2$\sqrt{2}$．
    故答案为：2$\sqrt{2}$．

    点评 本题考查双曲线的定义、方程和性质，考查内切圆的性质，考查定义法，属于中档题

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    5．函数f（x）=sinωx+$\sqrt{3}$cosωx+1的最小正周期为π，当x∈[m，n]时，f（x）至少有12个零点，则n-m的最小值为（　　）
    A．12πB．$\frac{7π}{3}$C．6πD．$\frac{16π}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．我们把三个集合中，通过两次连线后能够有关系的两个数字的关系称为”鼠标关系”，如图1，可称a与q，b与q，c与q都为”鼠标关系”集合A={a，b，c，d}，通过集合 B={1，2，3} 与集合C={m，n}最多能够产生24条”鼠标关系”，（只要有一条连线不同则”鼠标关系”不同）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．在复平面内，复数$\frac{2-i}{1-i}$（i是虚数单位）对应的点在（　　）
    A．第一象限B．第二象限C．第三象限D．第四象限

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．设等差数列{an}的前n项和为Sn，若2a3=3+a1，则S9的值为（　　）
    A．15B．27C．30D．40

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．下列命题中正确的是（　　）
    A．若p∨q为真命题，则p∧q为真命题
    B．“x=5”是“x2-4x-5=0”的充分不必要条件
    C．命题“若x＜-1，则x2-2x-3＞0”的否命题为：“若x＜-1，则x2-2x-3≤0”
    D．已知命题p：?x∈R，x2+x-1＜0，则￢p：?x∈R，x2+x-1≥0

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．一个几何体的三视图如图所示，则此几何体的体积为（　　）
    A．16B．36C．48D．72

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．在四棱锥P-ABCD中，底面ABCD是正方形，PA⊥底面ABCD，PA=AB，E，F，H分别是棱PA，PB，AD的中点，且过E，F，H的平面截四棱锥P-ABCD所得截面面积为$\frac{{3\sqrt{2}}}{2}$，则四棱锥P-ABCD的体积为（　　）
    A．$\frac{8}{3}$B．8C．$8\sqrt{3}$D．$24\sqrt{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．已知定圆M：（x-3）2+y2=16和圆M所在平面内一定点A，点P是圆M上一动点，线段PA的垂直平分线l交直线PM于点Q．
    （Ⅰ）讨论Q点的轨迹可能是下面的情形中的哪几种：①椭圆；②双曲线；③抛物线；④圆；⑤直线；⑥一个点．
    （Ⅱ）若定点A（5，0），试求△QMA的面积的最大值．

    查看答案和解析>>

    同步练习册答案