Question

17．在四棱锥P-ABCD中，底面ABCD是边长为2的正方形，且PA⊥平面ABCD，点M是棱PA的中点．
（1）若PA=4，求点C到平面BMD的距离；
（2）过直线BD且垂直于直线PC的平面交PC于点N，如果三棱锥N-BCD的体积取到最大值，求此时二面角M-ND-B的大小的余弦值．

Answer 1

分析 （1）设BD与AC相交于点O，连接MO，则BD⊥AC，证明平面BMD⊥平面PAC，过点A在平面PAC作AT⊥MO于点T，则AT⊥平面BMD，利用等面积，可求点C到平面BMD的距离；
（2）连接ON，则△ONC为直角三角形，设∠OCN=θ（0＜θ＜$\frac{π}{2}$），过N作NQ⊥OC于点Q，则NQ⊥平面ABCD，利用三棱锥N-BCD的体积取到最大值，确定AP=AC=2$\sqrt{2}$，以A为原点，分别以AB，AD，AP所在直线为x、y、z轴建立坐标系，求出平面MND的一个法向量、平面BND的一个法向量，利用向量的夹角公式，即可求此时二面角M-ND-B的大小的余弦值．

解答 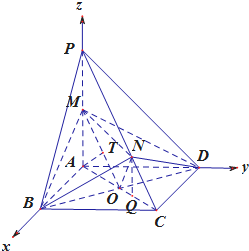解：（1）设BD与AC相交于点O，连接MO，则BD⊥AC，
∵PA⊥平面ABCD，BD?ABCD，
∴PA⊥BD，
∴PA∩AC=A，
∴BD⊥平面PAC，
∵BD?平面BMD，
∴平面BMD⊥平面PAC，
过点A在平面PAC作AT⊥MO于点T，则AT⊥平面BMD，
∴AT为点A到平面BMD的距离，
∵C，A到平面BMD的距离相等，
在△MAO中，AT=$\frac{AO•AM}{MO}$=$\frac{2\sqrt{3}}{3}$；
（2）连接ON，则△ONC为直角三角形，设∠OCN=θ（0＜θ＜$\frac{π}{2}$），过N作NQ⊥OC于点Q，则NQ⊥平面ABCD，
∴V_N-BCD=$\frac{1}{3}×\frac{1}{2}×2×2×NQ$=$\frac{2}{3}$NQ=$\frac{2}{3}$NCsinθ=$\frac{2}{3}$OC•cosθsinθ=$\frac{2}{3}$×$\frac{\sqrt{2}}{2}$sin2θ≤$\frac{\sqrt{2}}{3}$，
当且仅当θ=$\frac{π}{4}$时，V最大，此时AP=AC=2$\sqrt{2}$，
以A为原点，分别以AB，AD，AP所在直线为x、y、z轴建立坐标系，则有点$M（0，0，\sqrt{2}）、N（\frac{3}{2}，\frac{3}{2}，\frac{{\sqrt{2}}}{2}）、D（0，2，0）$、$C（2，2，0）、P（0，0，2\sqrt{2}），\overrightarrow{MD}=（0，2，-\sqrt{2}）、\overrightarrow{ND}=（-\frac{3}{2}，\frac{1}{2}，-\frac{{\sqrt{2}}}{2}）$，
设平面MND的一个法向量为$\overrightarrow{n_1}=（x，y，z）$，则有$\left\{\begin{array}{l}\overrightarrow{n_1}•\overrightarrow{ND}=0\\ \overrightarrow{n_1}•\overrightarrow{MD}=0\end{array}\right.⇒\left\{\begin{array}{l}2y-\sqrt{2}z=0\\-\frac{3}{2}x+\frac{1}{2}y-\frac{{\sqrt{2}}}{2}z=0\end{array}\right.$，取y=1，
则有$\overrightarrow{n_1}=（-\frac{1}{3}，1，\sqrt{2}）$，
∵直线PC⊥平面BND，∴平面BND的一个法向量为$\overrightarrow{PC}=（2，2，-2\sqrt{2}）$，易知二面角M-ND-B的平面角为锐角α，则$cosα=|{\frac{{\overrightarrow{n_1}•\overrightarrow{PC}}}{{|{\overrightarrow{n_1}}|•|{\overrightarrow{PC}}|}}}|=|{\frac{{-\frac{2}{3}+2-4}}{{\sqrt{\frac{1}{9}+1+2}•\sqrt{4+4+8}}}}|=\frac{{\sqrt{7}}}{7}$．

点评 本题考查平面与平面垂直的判定与性质，考查三棱锥N-BCD的体积取到最大值，求此时二面角M-ND-B的大小的余弦值，是中档题，解题时要注意空间思维能力的培养．