
分析 过点O分别作OE⊥AB于E,OF⊥AC于F,可得E、F分别是AB、AC的中点.根据Rt△AOE中余弦的定义,分别求出$\overrightarrow{AB}$•$\overrightarrow{AO}$=2,$\overrightarrow{AC}$•$\overrightarrow{AO}$=8,代入计算即可得出.
解答 解: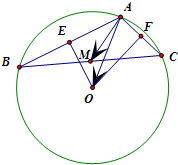 过点O分别作OE⊥AB于E,OF⊥AC于F,则E、F分别是AB、AC的中点
过点O分别作OE⊥AB于E,OF⊥AC于F,则E、F分别是AB、AC的中点
可得Rt△AEO中,cos∠OAE=$\frac{|\overrightarrow{AE|}}{|\overrightarrow{AO}|}$=$\frac{|\overrightarrow{AB}|}{2|\overrightarrow{AO}|}$
∴$\overrightarrow{AB}$•$\overrightarrow{AO}$=|$\overrightarrow{AB}$|•|$\overrightarrow{AO}$|•=$\frac{|\overrightarrow{AB}|}{2|\overrightarrow{AO}|}$=$\frac{1}{2}$|$\overrightarrow{AB}$|2=2,
同理可得$\overrightarrow{AC}$•$\overrightarrow{AO}$=$\frac{1}{2}$|$\overrightarrow{AC}$|2=8
∵M是BC边的中点,可得$\overrightarrow{AM}$=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AC}$),
∴$\overrightarrow{AO}•\overrightarrow{AM}$=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AC}$)•$\overrightarrow{AO}$=$\frac{1}{2}$($\overrightarrow{AB}$•$\overrightarrow{AO}$+$\overrightarrow{AC}$•$\overrightarrow{AO}$)=$\frac{1}{2}$×10=5,
故答案为:5
点评 本题为向量数量积的运算,数形结合并熟练应用数量积的定义是解决问题的关键,属中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{{\sqrt{3}π}}{4}$ | C. | $\frac{π}{8}$ | D. | $\frac{{\sqrt{3}π}}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -120 | B. | 120 | C. | -60 | D. | 60 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com