
抽奖游戏规则如下:一个口袋中装有完全一样的8个球,其中4个球上写有数字“5”,另外4个球上写有数字“10”.
(1)每次摸出一个球,记下球上的数字后放回,求抽奖者四次摸球数字之和为30的概率;
(2)若抽奖者每交2元钱(抽奖成本)获得一次抽奖机会,每次摸出4个球,若4个球数字之和为20或40则中一等奖,奖励价值20元的商品一件;若4个球数字之和为25或35则中二等奖,奖励价值2元的商品一件;若4个球数字之和为30则不中奖.试求抽奖者收益ξ(奖品价值﹣抽奖成本)的期望.
(1) ;(2)
;(2)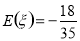
【解析】
试题分析:(1)求随机变量的分布列的主要步骤:一是明确随机变量的取值,并确定随机变量服从何种概率分布;二是求每一个随机变量取值的概率,三是列成表格;(2)求出分布列后注意运用分布列的两条性质检验所求的分布列是否正确;(3)求解离散随机变量分布列和方差,首先要理解问题的关键,其次要准确无误的找出随机变量的所有可能值,计算出相对应的概率,写成随机变量的分布列,正确运用均值、方差公式进行计算;(4)数学期望是离散型随机变量的一个特征数,它反映了离散型随机变量取值的平均水平,二项分布的期望和方差:若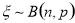 ,则
,则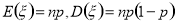 .
.
试题解析:【解析】
(1)由题意,每次摸球写有数字“5”的概率为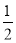 . 1分
. 1分
四次摸球数字之和为30,只能是两次摸到写有数字“5”,另两次写有数字“10”. 2分
设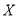 为4次摸球中写有数字“5”的次数,则
为4次摸球中写有数字“5”的次数,则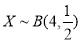 , 3分
, 3分
所以抽奖者四次摸球数字之和为30的概率为: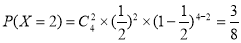 . 5分
. 5分
(2)由题意,抽奖者获得的收益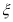 可取18元、0元、-2元. 6分
可取18元、0元、-2元. 6分
从8个球中任取4个球的结果数为 ,其中恰好有
,其中恰好有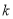 个球写有数字“5”的结果数为
个球写有数字“5”的结果数为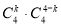 ,
,
所以从8个球中任取4个球,其中恰好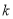 个球写有数字“5”的概率为:
个球写有数字“5”的概率为:
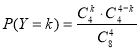 ,
, , 8分
, 8分
所以 , 9分
, 9分
 , 10分
, 10分
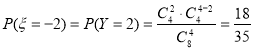 , 11分
, 11分
因此,随机变量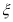 的分布列为
的分布列为
| 18 | 0 | -2 |
|
|
|
|
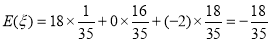 . 13分
. 13分
所以,(1)抽奖者四次摸球数字之和为30的概率为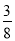 ;(2) 抽奖者收益的期望为
;(2) 抽奖者收益的期望为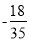 元. 14分
元. 14分
考点:(1)求随机事件发生的概率;(2)求随机事件的数学期望.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2015届广东省高三上学期暑假联考文科数学试卷(解析版) 题型:选择题
若某程序框图如图1所示,则输出的n的值是 ( )
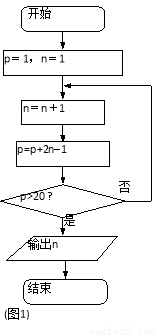
A. 3 B.4 C. 5 D. 6
查看答案和解析>>
科目:高中数学 来源:2015届广东省广州市高三上学期第一次质量检测理科数学试卷(解析版) 题型:选择题
已知向量 与
与 的夹角为120°,且
的夹角为120°,且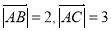 ,若
,若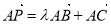 ,且
,且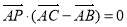 ,则实数
,则实数 的值为( )
的值为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届广东省广州市高三上学期第一次质量检测文科数学试卷(解析版) 题型:选择题
定义在R上的函数f(x)满足f(x)= 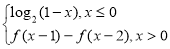 ,则f(2015)的值为( )
,则f(2015)的值为( )
A.-1 B.0 C.1 D.2
查看答案和解析>>
科目:高中数学 来源:2015届广东省广州市高三上学期第一次质量检测文科数学试卷(解析版) 题型:选择题
“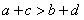 ”是“
”是“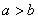 且
且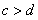 ”的( )
”的( )
A.必要不充分条件 B.充分不必要条件
C.充分必要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2015届广东省东莞市高二下学期期末理科数学试卷(解析版) 题型:选择题
已知实数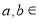 {1,3,5,7},那么
{1,3,5,7},那么 的不同值有( )
的不同值有( )
A.12个 B.13个 C.16个 D.17个
查看答案和解析>>
科目:高中数学 来源:2015届广东省东莞市高三上学期第二次月考理科数学试卷(解析版) 题型:填空题
某学校高一、高二、高三年级的学生人数之比为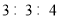 ,现用分层抽样的方法从该校高中三个年级的学生中抽取容量为50的样本,则应从高一年级抽取
,现用分层抽样的方法从该校高中三个年级的学生中抽取容量为50的样本,则应从高一年级抽取
查看答案和解析>>
科目:高中数学 来源:2015届广东惠州市高三第二次调研考试文科数学试卷(解析版) 题型:选择题
某学校要召开学生代表大会,规定各班每10人推选一名代表,当各班人数除以10的余数大于6时再增选一名代表.那么,各班可推选代表人数 与该班人数
与该班人数 之间的函数关系用取整函数
之间的函数关系用取整函数 (
( 表示不大于
表示不大于 的最大整数)可以表示为 ( )
的最大整数)可以表示为 ( )
A.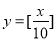 B.
B.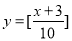 C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com