
.如图(一),在直角梯形ABCD中,AD∥BC,AB⊥AD,AD=2AB=2BC,E为AD中点,沿CE折叠,使平面DEC⊥平面ABCE,如图(二).
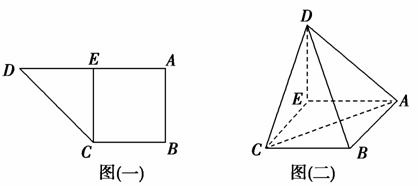
(1)证明:AC⊥BD
(2)求DE与平面ACD所成角的余弦值.
方法1:(1)证明:由题意知DE⊥平面ABCE,则DE⊥AC,
连接BE,由四边形ABCE是正方形可知AC⊥BE.
又DE∩BE=E,DE,BE⊂平面DEB,∴AC⊥平面DEB.
又DB⊂平面DEB.∴AC⊥BD.
(2)连接BE交AC于O,连接DO,
由(1)知AC⊥平面DEB,AC⊂平面ADC,
∴平面EDO⊥平面ADC,且交线为DO.
∴DE在平面ADC内的射影为DO.
∴∠EDO就是DE与平面ACD所成的角.
在△DEO中,∠DEO=90°,
设BC=a,则EO= a,DE=a,DO=
a,DE=a,DO=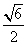 a,
a,
∴cos∠EDO= =
= ,
,
即DE与平面ACD所成角的余弦值为 .
.
方法2:

如图所示,以E为原点,EC、EA、ED所在直线分别为x轴、y轴、z轴建立空间直角坐标系E-xyz,
令AB=a,则E(0,0,0),C(a,0,0),A(0,a,0),D(0,0,a),B(a,a,0), =(a,-a,0),
=(a,-a,0),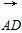 =(0,-a,a),
=(0,-a,a),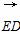 =(0,0,a),
=(0,0,a), =(a,a,-a).
=(a,a,-a).
(1)证明:∵ =(a,-a,0)·(a,a,-a)=0,
=(a,-a,0)·(a,a,-a)=0,
∴ ,即AC⊥DB.
,即AC⊥DB.
(2)设平面ACD的法向量n=(x,y,1),
则
∴n=(1,1,1),
 设DE与平面ACD所成的角为θ,
设DE与平面ACD所成的角为θ,
则sinθ=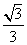 ,∴cosθ=
,∴cosθ= =
= ,
,
∴DE与平面ACD所成角的余弦值为 .
.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:高中数学 来源: 题型:
若直线l1、l2的方向向量分别为a=(2,4,-4),b=(-6,9,6),则( )
A.l1∥l2 B.l1⊥l2
C.l1与l2相交但不垂直 D.以上均不正确
查看答案和解析>>
科目:高中数学 来源: 题型:
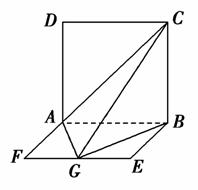
如图,平面ABCD⊥平面ABEF,四边形ABCD是正方形,四边形ABEF是矩形,且AF=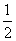 AD=a,G是EF的中点,则GB与平面AGC所成角的正弦值为( )
AD=a,G是EF的中点,则GB与平面AGC所成角的正弦值为( )
A.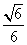 B.
B.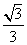
C. D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知三边长分别为3、4、5的△ABC的外接圆恰好是球O的一个大圆,P为球面上一点,若点P到△ABC的三个顶点的距离相等,则三棱锥P-ABC的体积为( )
A.5 B.10
C.20 D.30
查看答案和解析>>
科目:高中数学 来源: 题型:
在空间中,有如下命题:
①互相平行的两条直线在同一个平面内的射影必然是互相平行的两条直线;
②若平面α∥平面β,则平面α内任意一条直线m∥平面β;
③若平面α与平面β的交线为m,平面α内的直线n⊥直线m,则直线n⊥平面β;
④若平面α内的三点A、B、C到平面β的距离相等,则α∥β.
其中正确命题的序号为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com