
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,椭圆上任意一点到右焦点
,椭圆上任意一点到右焦点![]() 的距离的最大值为
的距离的最大值为![]() .
.
(1)求椭圆的方程;
(2)已知点![]() 是线段
是线段![]() 上异于
上异于![]() 的一个定点(
的一个定点(![]() 为坐标原点),是否存在过点
为坐标原点),是否存在过点![]() 且与
且与![]() 轴不垂直的直线
轴不垂直的直线![]() 与椭圆交于
与椭圆交于![]() 两点,使得
两点,使得![]() ,并说明理由.
,并说明理由.
【答案】(1)![]() (2)当
(2)当![]() 时,
时,![]() ,即存在这样的直线
,即存在这样的直线![]() ;当
;当![]() 时,
时,![]() 不存在,即不存在这样的直线
不存在,即不存在这样的直线![]() .
.
【解析】
试题分析:(I)根据题意建立关于a、b、c的方程组,解之可得a= ![]() 且b=1,从而得到该椭圆的标准方程;(II)根据题意设直线l其方程为y=k(x-1),直线方程与椭圆消去y得关于x的一元二次方程,利用根与系数的关系得A
且b=1,从而得到该椭圆的标准方程;(II)根据题意设直线l其方程为y=k(x-1),直线方程与椭圆消去y得关于x的一元二次方程,利用根与系数的关系得A ![]() 、B
、B ![]() 满足
满足![]() ,从而得到AB的中点为M
,从而得到AB的中点为M  ,由|AC|=|BC|得CM⊥AB,利用斜率之积为-1建立关于k、m的关系式,整理后加以讨论即可得答案
,由|AC|=|BC|得CM⊥AB,利用斜率之积为-1建立关于k、m的关系式,整理后加以讨论即可得答案
试题解析:(1) ∵ ,∴
,∴ ,∴
,∴![]() ,
,
∴椭圆的方程为![]() .
.
(2) 由(1)得![]() ,∴
,∴![]() ,假设存在满足题意的直线
,假设存在满足题意的直线![]() ,设
,设![]() 为
为![]() ,
,
代入![]() ,得
,得![]() .
.
设![]() ,则
,则![]() ,
,
∴![]() .
.
设![]() 的中点为
的中点为![]() ,则
,则![]() .
.
∵![]() ,∴
,∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴当![]() 时,
时,![]() ,即存在这样的直线
,即存在这样的直线![]() ;
;
当![]() 时,
时,![]() 不存在,即不存在这样的直线
不存在,即不存在这样的直线![]() .
.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:高中数学 来源: 题型:
【题目】某单位最近组织了一次健身活动,活动分为登山组和游泳组,且每个职工至多参加了其中一组,在参加活动的职工中,青年人占42.5%,中年人占47.5%,老年人占10%.登山组的职工占参加活动总人数的![]() ,且该组中,青年人占50%,中年人占40%,老年人占10%.为了了解各组不同年龄层次的职工对本次活动的满意程度,现用分层抽样方法从参加活动的全体职工中抽取一个容量为200的样本,试确定:
,且该组中,青年人占50%,中年人占40%,老年人占10%.为了了解各组不同年龄层次的职工对本次活动的满意程度,现用分层抽样方法从参加活动的全体职工中抽取一个容量为200的样本,试确定:
(1)游泳组中,青年人、中年人、老年人分别所占的比例;
(2)游泳组中,青年人、中年人、老年人分别应抽取的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于![]() 的不等式
的不等式![]() .
.
(1)是否存在![]() 使对所有的实数
使对所有的实数![]() ,不等式恒成立?若存在,求出
,不等式恒成立?若存在,求出![]() 的取值范围;若不存在,请说明理由;
的取值范围;若不存在,请说明理由;
(2)设不等式对于满足![]() 的一切
的一切![]() 的值都成立,求
的值都成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() .
.
(Ⅰ)当![]() 时,求曲线
时,求曲线![]() 在
在![]() 处的切线的方程;
处的切线的方程;
(Ⅱ)如果存在![]() ,使得
,使得![]() 成立,求满足上述条件的最大整数
成立,求满足上述条件的最大整数![]() ;
;
(Ⅲ)如果对任意的![]() ,都有
,都有![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱锥A-BCD中,AB⊥平面BCD,CD⊥BD .
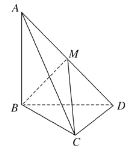
(1)求证:CD⊥平面ABD;
(2)若AB=BD=CD=1,M为AD中点,求三棱锥A-MBC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某小区随机抽取40个家庭,收集了这40个家庭去年的月均用水量(单位:吨)的数据,整理得到频数分布表和频率分布直方图.
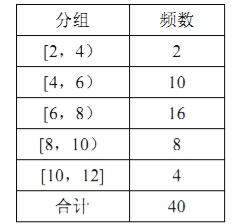
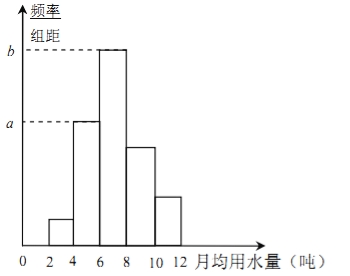
(1)求频率分布直方图中![]() 的值;
的值;
(2)从该小区随机选取一个家庭,试估计这个家庭去年的月均用水量不低于6吨的概率;
(3)在这40个家庭中,用分层抽样的方法从月均用水量不低于6吨的家庭里抽取一个容量为7的样本,将该样本看成一个总体,从中任意选取2个家庭,求其中恰有一个家庭的月均用水量不低于8吨的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市100户居民的月平均用电量(单位:度),以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组的频率分布直方图如图:
分组的频率分布直方图如图:
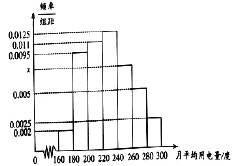
(Ⅰ)求直方图中![]() 的值;
的值;
(Ⅱ)求月平均用电量的众数和中位数;
(Ⅲ)在月平均用电量为![]() ,
,![]() ,
,![]() ,
,![]() 的四组用户中,用分层抽样的方法抽取11户居民,则月平均用电量在
的四组用户中,用分层抽样的方法抽取11户居民,则月平均用电量在![]() 的用户中应抽取多少户?
的用户中应抽取多少户?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com