
在△ABC中,a,b,c分别是角A,B,C的对边,a,b,c满足b2=a2+c2-ac,若AC=2 ,则△ABC面积的最大值为( )
,则△ABC面积的最大值为( )
A.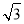 B.2
B.2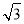 C.3
C.3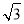 D.4
D.4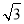
科目:高中数学 来源:2015高考数学(理)一轮配套特训:4-3平面向量的数量积及应用(解析版) 题型:填空题
已知向量m=(a,b),n=(c,d),p=(x,y),定义新运算m?n=(ac+bd,ad+bc),其中等式右边是通常的加法和乘法运算.如果对于任意向量m都有m?p=m成立,则向量p=________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:4-1向量的概念及运算(解析版) 题型:选择题
如图,在△OAB中,P为线段AB上的一点,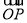 =x
=x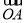 +y
+y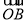 ,且
,且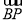 =2
=2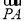 ,则( )
,则( )

A.x=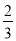 ,y=
,y=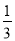 B.x=
B.x= ,y=
,y=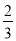
C.x=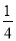 ,y=
,y= D.x=
D.x=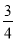 ,y=
,y=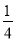
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-8解三角形应用举例(解析版) 题型:选择题
在200 m高的山顶上,测得山下一塔顶与塔底俯角分别为30°、60°,则塔高为( )
A.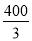 m B.
m B.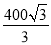 m C.
m C.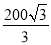 m D.
m D.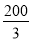 m
m
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-7正弦定理和余弦定理(解析版) 题型:解答题
在△ABC中,内角A,B,C的对边分别为a,b,c.已知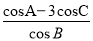 =
= .
.
(1)求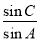 的值;
的值;
(2)若B为钝角,b=10,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-7正弦定理和余弦定理(解析版) 题型:选择题
在△ABC中,已知sinA∶sinB∶sinC=4∶5∶8,则△ABC一定为( )
A.正三角形 B.等腰三角形
C.直角三角形 D.钝角三角形
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-6简单的三角恒等变换(解析版) 题型:解答题
已知α,β∈(0,π),且tan(α-β)=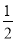 ,tanβ=-
,tanβ=- ,求2α-β的值.
,求2α-β的值.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-5两角和与差的正弦、余弦和正切(解析版) 题型:填空题
已知13sinα+5cosβ=9,13cosα+5sinβ=15,那么sin(α+β)的值为________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-9函数模型及其应用(解析版) 题型:解答题
某工厂生产一种产品的原材料费为每件40元,若用x表示该厂生产这种产品的总件数,则电力与机器保养等费用为每件0.05x元,又该厂职工工资固定支出12500元.
(1)把每件产品的成本费P(x)(元)表示成产品件数x的函数,并求每件产品的最低成本费;
(2)如果该厂生产的这种产品的数量x不超过3000件,且产品能全部销售,根据市场调查:每件产品的销售价Q(x)与产品件数x有如下关系:Q(x)=170-0.05x,试问生产多少件产品时,总利润最高?(总利润=总销售额-总成本)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com