
在△ABC中,已知sinA∶sinB∶sinC=4∶5∶8,则△ABC一定为( )
A.正三角形 B.等腰三角形
C.直角三角形 D.钝角三角形
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源:2015高考数学(理)一轮配套特训:4-3平面向量的数量积及应用(解析版) 题型:解答题
设向量a,b满足|a|=|b|=1及|3a-2b|= .
.
(1)求a,b夹角的大小;
(2)求|3a+b|的值.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-8解三角形应用举例(解析版) 题型:填空题
甲船在岛B的正南A处,AB=10 n mile,甲船自A处以4 n mile/h的速度向正北航行,同时乙船以6 n mile/h的速度自岛B出发,向北偏东60°方向驶去,则两船相距最近时经过了________ min.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-7正弦定理和余弦定理(解析版) 题型:选择题
已知△ABC的三边长为a,b,c,且面积S△ABC= (b2+c2-a2),则A=( )
(b2+c2-a2),则A=( )
A.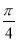 B.
B.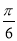 C.
C.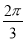 D.
D.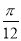
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-7正弦定理和余弦定理(解析版) 题型:选择题
在△ABC中,a,b,c分别是角A,B,C的对边,a,b,c满足b2=a2+c2-ac,若AC=2 ,则△ABC面积的最大值为( )
,则△ABC面积的最大值为( )
A.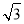 B.2
B.2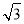 C.3
C.3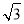 D.4
D.4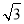
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-6简单的三角恒等变换(解析版) 题型:解答题
已知函数f(x)=cos2ωx+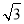 sinωxcosωx-
sinωxcosωx-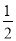 (ω>0)的最小正周期为π.
(ω>0)的最小正周期为π.
(1)求ω值及f(x)的单调递增区间;
(2)在△ABC中,a,b,c分别是角A,B,C的对边,已知a=1,b=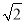 ,f(
,f(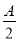 )=
)=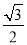 ,求角C的大小.
,求角C的大小.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-6简单的三角恒等变换(解析版) 题型:选择题
将函数f(x)=cos2x-sin2x的图象向左平移 个单位后得到函数F(x)的图象,则下列说法中正确的是( )
个单位后得到函数F(x)的图象,则下列说法中正确的是( )
A.函数F(x)是奇函数,最小值是-2
B.函数F(x)是偶函数,最小值是-2
C.函数F(x)是奇函数,最小值是-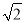
D.函数F(x)是偶函数,最小值是-
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-5两角和与差的正弦、余弦和正切(解析版) 题型:选择题
已知 =5,则sin2α-sinαcosα的值是( )
=5,则sin2α-sinαcosα的值是( )
A. B.-
B.-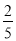 C.-2 D.2
C.-2 D.2
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-9函数模型及其应用(解析版) 题型:选择题
某种新药服用x小时后血液中的残留量为y毫克,如图所示为函数y=f(x)的图象,当血液中药物残留量不小于240毫克时,治疗有效.设某人上午8:00第一次服药,为保证疗效,则第二次服药最迟的时间应为( )
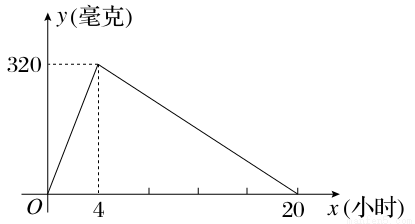
A.上午10:00 B.中午12:00
C.下午4:00 D.下午6:00
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com