
 上,并且同时满足以下两个条件的函数
上,并且同时满足以下两个条件的函数 称为
称为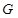 函数.
函数. ,总有
,总有 ;
; 时,总有
时,总有 成立.
成立. 与
与 是定义在
是定义在 上的函数.
上的函数. 是否为
是否为 函数?并说明理由;
函数?并说明理由; 是
是 函数,求实数
函数,求实数 的值;
的值; ,使方程
,使方程 恰有两解?若存在,求出实数
恰有两解?若存在,求出实数 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.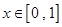 时,总有
时,总有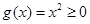 满足①……………………………1分
满足①……………………………1分 时,
时,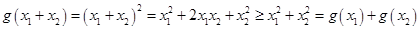 满足②………3分
满足②………3分 为
为 函数;………………………………………………………4分
函数;………………………………………………………4分 是
是 函数,根据①有
函数,根据①有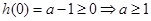 ,……………6分
,……………6分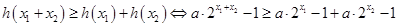
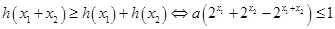
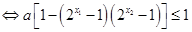 …………………………………………………7分
…………………………………………………7分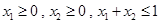 ,
,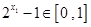 ,
,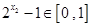 ,其中
,其中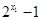 和
和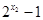 不能同时取到
不能同时取到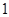 ,
,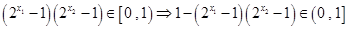 ,……………………9分
,……………………9分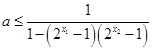 ,即
,即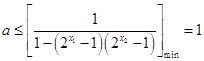 ,……………10分
,……………10分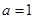 …………………………………………………………………………11分
…………………………………………………………………………11分 是
是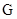 函数,根据①有
函数,根据①有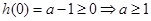 ,…………6分
,…………6分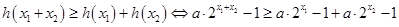
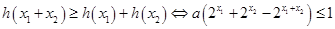 ………………………………8分
………………………………8分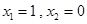 得
得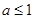 …………………………………………………………10分
…………………………………………………………10分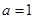 …………………………………………………………………………11分
…………………………………………………………………………11分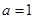 ,原方程可以化为
,原方程可以化为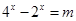 ,……………12分
,……………12分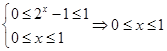 ,……………………………………………………14分
,……………………………………………………14分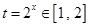 ,则
,则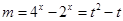 ,………………………………………15分
,………………………………………15分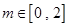 时,方程有一解;…………………………………16分
时,方程有一解;…………………………………16分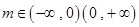 时,方程无解;…………………………17分
时,方程无解;…………………………17分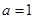 ,原方程可以化为
,原方程可以化为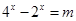 ,…………………12分
,…………………12分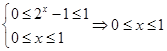 ,……………………………………………………14分
,……………………………………………………14分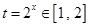 ,…………………………………………………………………15分
,…………………………………………………………………15分 ,……………………………………………16分
,……………………………………………16分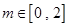 时,方程有解。……………………………………………18分
时,方程有解。……………………………………………18分

科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 g(x)=
g(x)= ,则函数h(x)= f (x)·g(x)
,则函数h(x)= f (x)·g(x)| A.是奇函数但不是偶函数 | B.是偶函数但不是奇函数 |
| C.既是奇函数也是偶函数 | D.既不是偶函数也不是奇函数 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 时小白鼠将会死亡,注射这种抗癌药物可杀死其体内癌细胞的
时小白鼠将会死亡,注射这种抗癌药物可杀死其体内癌细胞的 .
.天数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … |
癌细胞个数 | 1 | 2 | 4 | 8 | 16 | 32 | 64 | … |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 是定义在R上的增函数,则下列结论一定正确的是( )
是定义在R上的增函数,则下列结论一定正确的是( )A. 是偶函数且是增函数 是偶函数且是增函数 | B. 是偶函数且是减函数 是偶函数且是减函数 |
C. 是奇函数且是增函数 是奇函数且是增函数 | D.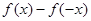 是奇函数且是减函数 是奇函数且是减函数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com