
【题目】如图①:在平行四边形![]() 中,
中,![]() ,
,![]() ,将
,将![]() 沿对角线
沿对角线![]() 折起,使
折起,使![]() ,连结
,连结![]() ,得到如图②所示三棱锥
,得到如图②所示三棱锥![]() .
.
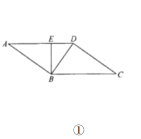
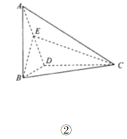
(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() ,二面角
,二面角![]() 的平面角的正切值为
的平面角的正切值为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)证明![]() ,从而证明
,从而证明![]() 平面
平面![]() ,进而得出
,进而得出![]() ,即可证
,即可证![]() 平面
平面![]() .最后证得
.最后证得![]() 平面
平面![]() .
.
(2)若![]() ,二面角
,二面角![]() 的平面角的正切值为
的平面角的正切值为![]() ,由(1)知
,由(1)知![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() 即为二面角
即为二面角![]() 的平面角,得
的平面角,得![]() ,从而求出
,从而求出![]() ,
,![]() ,建立空间直角坐标系,求平面
,建立空间直角坐标系,求平面![]() 的法向量为
的法向量为![]() ,
,
最后根据公式![]() ,即得直线
,即得直线![]() 与平面
与平面![]() 所成角大小.
所成角大小.
(1)证明:在平行四边形![]() 中,
中,![]() ,
,
则![]() .
.
在三棱锥![]() 中,因为
中,因为![]() ,
,![]() .
.
所以![]() 平面
平面![]() ,所以
,所以![]() .
.
又![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,所以
,所以![]() .
.
因为![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)解:由(1)知![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() 即为二面角
即为二面角![]() 的平面角,即
的平面角,即![]() .
.
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
所以![]() ,故
,故![]() ,
,
又![]() .所以
.所以![]() .
.
在平行四边形![]() ,
,![]() ,
,![]() ,
,
所以![]() 与
与![]() 为相似三角形,则
为相似三角形,则![]() ,
,
故![]() (
(![]() ),解得
),解得![]() ,
,
故![]() ,解得
,解得![]() ,
,
所以![]() ,
,![]() .
.
过点![]() 作
作![]() ,以
,以![]() 为坐标原点,
为坐标原点,![]() ,
,![]() ,
,![]() 的方向为
的方向为![]() 轴、
轴、![]() 轴、
轴、![]() 轴的正方向,建立空间直角坐标系,如图所示.
轴的正方向,建立空间直角坐标系,如图所示.
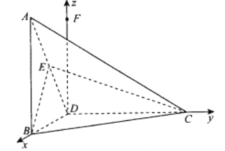
则![]() ,
,![]() ,
,![]() ,
,![]() .
.
所以![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则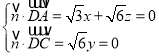
令![]() ,得
,得![]() .
.
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
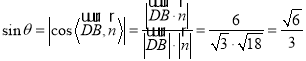
即直线![]() 与平面
与平面![]() 所成角为
所成角为![]() .
.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:
【题目】某物流公司专营从甲地到乙地的货运业务(货物全部用统一规格的包装箱包装),现统计了最近100天内每天可配送的货物量,按照可配送货物量T(单位:箱)分成了以下几组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,并绘制了如图所示的频率分布直方图(同一组数据用该组数据的区间中点值作代表,将频率视为概率).
,并绘制了如图所示的频率分布直方图(同一组数据用该组数据的区间中点值作代表,将频率视为概率).
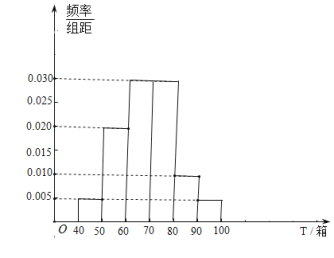
(1)该物流公司负责人决定用分层抽样的方法从前3组中随机抽出11天的数据来分析可配送货物量少的原因,并从这11天的数据中再抽出3天的数据进行财务分析,求这3天的数据中至少有2天的数据来自![]() 这一组的概率.
这一组的概率.
(2)由频率分布直方图可以认为,该物流公司每日的可配送货物量T(单位:箱)服从正态分布![]() ,其中
,其中![]() 近似为样本平均数.
近似为样本平均数.
(ⅰ)试利用该正态分布,估计该物流公司2000天内日货物配送量在区间![]() 内的天数(结果保留整数).
内的天数(结果保留整数).
(ⅱ)该物流公司负责人根据每日的可配送货物量为公司装卸货物的员工制定了两种不同的工作奖励方案.
方案一:直接发放奖金,按每日的可配送货物量划分为以下三级:![]() 时,奖励50元;
时,奖励50元;![]() ,奖励80元;
,奖励80元;![]() 时,奖励120元.
时,奖励120元.
方案二:利用抽奖的方式获得奖金,其中每日的可配送货物量不低于![]() 时有两次抽奖机会,每日的可配送货物量低于
时有两次抽奖机会,每日的可配送货物量低于![]() 时只有一次抽奖机会,每次抽奖的奖金及对应的概率分别为
时只有一次抽奖机会,每次抽奖的奖金及对应的概率分别为
奖金 | 50 | 100 |
概率 |
|
|
小张恰好为该公司装卸货物的一名员工,试从数学期望的角度分析,小张选择哪种奖励方案对他更有利?
附:若![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() 为
为![]() 中点,下列说法中
中点,下列说法中
(1)![]() ;
;
(2)记二面角![]() 的平面角分别为
的平面角分别为![]() ;
;
(3)记![]() 的面积分别为
的面积分别为![]() ;
;
(4)![]() ,
,
正确说法的个数为( )

A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知斜率存在且不为0的直线![]() 过点
过点![]() ,设直线
,设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,椭圆
两点,椭圆![]() 的左顶点为
的左顶点为![]() .
.
(1)若![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)若直线![]() 分别交直线
分别交直线![]() 于点
于点![]() ,且
,且![]() ,记直线
,记直线![]() 的斜率分别为
的斜率分别为![]() .探究:
.探究:![]() 是否为定值?若是,求出该定值;若不是,请说明理由.
是否为定值?若是,求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为配合“2019双十二”促销活动,某公司的四个商品派送点如图环形分布,并且公司给![]() 四个派送点准备某种商品各50个.根据平台数据中心统计发现,需要将发送给
四个派送点准备某种商品各50个.根据平台数据中心统计发现,需要将发送给![]() 四个派送点的商品数调整为40,45,54,61,但调整只能在相邻派送点进行,每次调动可以调整1件商品.为完成调整,则( )
四个派送点的商品数调整为40,45,54,61,但调整只能在相邻派送点进行,每次调动可以调整1件商品.为完成调整,则( )

A.最少需要16次调动,有2种可行方案
B.最少需要15次调动,有1种可行方案
C.最少需要16次调动,有1种可行方案
D.最少需要15次调动,有2种可行方案
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的正方形,
的正方形,![]() 是正三角形,CD平面PAD,E,F,G,O分别是PC,PD,BC,AD 的中点.
是正三角形,CD平面PAD,E,F,G,O分别是PC,PD,BC,AD 的中点.

(Ⅰ)求证:PO平面![]() ;
;
(Ⅱ)求平面EFG与平面![]() 所成锐二面角的大小;
所成锐二面角的大小;
(Ⅲ)线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,若存在,求线段
,若存在,求线段![]() 的长度;若不存在,说明理由.
的长度;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com