已知MOD函数是一个求余数的函数.其格式为MOD(n.m).其结果为n除以m的余数.例如MOD(8.3)=2．如图是一个算法的程序框图.当输入n=25时.则输出的结果为( )A．4B．5C．6D．7 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

19．

已知MOD函数是一个求余数的函数，其格式为MOD（n，m），其结果为n除以m的余数，例如MOD（8，3）=2．如图是一个算法的程序框图，当输入n=25时，则输出的结果为（　　）

A．

B．

C．

D．

分析模拟执行程序框图，根据题意，依次计算MOD（n，i）的值，当i=5，MOD（25，5）=0，满足条件MOD（25，2）=0，退出循环，输出i的值为5．

解答解：模拟执行程序框图，可得：
n=25，i=2，MOD（25，2）=1，
不满足条件MOD（25，2）=0，i=3，MOD（25，3）=1，
不满足条件MOD（25，3）=0，i=4，MOD（25，4）=1，
不满足条件MOD（25，4）=0，i=5，MOD（25，5）=0，
满足条件MOD（25，2）=0，退出循环，输出i的值为5．
故选：B．

点评本题主要考查了循环结构的程序框图，依次正确写出每次循环得到的MOD（n，i）的值是解题的关键，属于基础题．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：填空题

9．已知f（x）=lnx-x²+x+2，g（x）=x³-（1+2e）x²+（m+1）x+2，（m∈R），讨论f（x）与g（x）交点的个数．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

10．

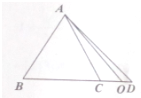如图，在△ABC中，点D是BC延长线上的点，$\overline{BC}$=3$\overline{CD}$，O在线段CD上且不与端点重合，若$\overrightarrow{AO}$=x$\overrightarrow{AB}$+（1-x）$\overrightarrow{AC}$，则x的取值范围是（$-\frac{1}{3}$，0）．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

7．若向量$\overrightarrow{a}$=（3，m），$\overrightarrow{b}$=（2，-1），$\overrightarrow{a}$∥$\overrightarrow{b}$，则实数m的值为（　　）

A．

-$\frac{3}{2}$

B．

$\frac{3}{2}$

C．

D．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

14．若在圆C：x²+（y-a）²=4上有且仅有两个点到原点O距离为1，则实数a的取值范围是-3＜a＜-1或1＜a＜3．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

4．为了分流地铁高峰的压力，某市发改委通过听众会，决定实施低峰优惠票价制度．不超过22公里的地铁票价如下表：

乘坐里程x（单位：km）	0＜x≤6	6＜x≤12	12＜x≤22
票价（单位：元）	3	4	5

现有甲、乙两位乘客，他们乘坐的里程都不超过22公里．已知甲、乙乘车不超过6公里的概率分别为$\frac{1}{4}$，$\frac{1}{3}$，甲、乙乘车超过6公里且不超过12公里的概率分别为$\frac{1}{2}$，$\frac{1}{3}$．
（Ⅰ）求甲、乙两人所付乘车费用不相同的概率；
（Ⅱ）设甲、乙两人所付乘车费用之和为随机变量ξ，求ξ的分布列与数学期望．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

11．已知函数f（x）=2sin（2x+φ）（|φ|＜$\frac{π}{2}）$的图象过点$（0，\sqrt{3}）$，则f（x）的图象的一个对称中心是（　　）

A．

$（-\frac{π}{3}，0）$

B．

$（-\frac{π}{6}，0）$

C．

$（\frac{π}{6}，0）$

D．

$（\frac{π}{4}，0）$

查看答案和解析>>