
 如图所示,直角三角形ABC中,∠ACB=90°,AC=2,BC=2
如图所示,直角三角形ABC中,∠ACB=90°,AC=2,BC=2| 2 |
| A、90° | B、45° |
| C、60° | D、30° |
 解:以C为原点,CA为x轴,CB为y轴,CP为z轴,
解:以C为原点,CA为x轴,CB为y轴,CP为z轴,| 2 |
| 2 |
| PE |
| 2 |
| n |
| PE |
| n |
| -3 | ||
|
| ||
| 2 |


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:
 如图,平面α⊥平面β,α∩β=直线l,A,C是α内不同的两点,B,D是β内不同的两点,且A,B,C,D∈直线l,M,N分别是线段AB,CD的中点.下列判断正确的是( )
如图,平面α⊥平面β,α∩β=直线l,A,C是α内不同的两点,B,D是β内不同的两点,且A,B,C,D∈直线l,M,N分别是线段AB,CD的中点.下列判断正确的是( )| A、当CD=2AB时,M,N两点不可能重合 |
| B、当AB,CD是异面直线时,直线MN可能与l平行 |
| C、当AB与CD相交,直线AC平行于l时,直线BD可以与l相交 |
| D、M,N两点可能重合,但此时直线AC与l不可能相交 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| e1 |
| e2 |
| b |
| e1 |
| e2 |
| c |
| 1 |
| 2 |
| e1 |
| 3 |
| 2 |
| e2 |
| e1 |
| e2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
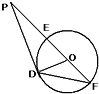 如图,已知P是⊙O外一点,PD为⊙O的切线,D为切点,割线PEF经过圆心O.若PF=16,PD=4
如图,已知P是⊙O外一点,PD为⊙O的切线,D为切点,割线PEF经过圆心O.若PF=16,PD=4| 3 |
| A、13 | B、6.5 | C、7 | D、8 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图是正方体的表面展开图,在这个正方体中有如下命题:
如图是正方体的表面展开图,在这个正方体中有如下命题:| A、3个 | B、2个 | C、1个 | D、0个 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 3 |
| π |
| 3 |
A、周期为
| ||||
B、周期为
| ||||
C、最大值为2,一个对称轴为x=
| ||||
D、最大值为1,一个对称轴为x=
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| 4 |
| y2 |
| 3 |
| PQ |
| F1P |
| PQ |
| PF2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com