
分析 (1)利用等差数列的通项公式即可得出.
(2)利用等比数列的通项公式及其前n项和公式即可得出.
解答 解:(1)由题意可知:$\left\{\begin{array}{l}{a_1}+({{a_1}+d})={a_1}+2d①\\{a_1}•({{a_1}+d})={a_1}+3d②\end{array}\right.$
由①式可知a1=d,代入②式,得:d•2d=d+3d,即:d2-2d=0,
解得:d1=0,d2=2.
当d=0时,an=a1=0.
当d=2时,an=a1+(n-1)d=2+(n-1)×2=2n.
∴an=0.或者an=2n.
(2)由${S_3}={b_1}+{b_1}q+{b_1}{q^2}=2(1+q+{q^2})=6$q2+q-2=0解得:q=-2,或q=1,
∴Sn=2n或者${S_n}=\frac{2}{3}×[{1-{{({-2})}^n}}]$.
点评 本题考查了等差数列与等比数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 16,$\sqrt{3}$ | B. | 18,$\sqrt{3}$ | C. | 16,$3\sqrt{3}$ | D. | 18,$3\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
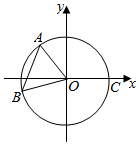 如图,点A,B是单位圆上的两点,点C是圆与x轴正半轴的交点,若点A的坐标为(-$\frac{3}{5}$,$\frac{4}{5}$),记∠COA=α,且△AOB是正三角形.
如图,点A,B是单位圆上的两点,点C是圆与x轴正半轴的交点,若点A的坐标为(-$\frac{3}{5}$,$\frac{4}{5}$),记∠COA=α,且△AOB是正三角形.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5$\sqrt{3}$ | B. | 5 | C. | 5$\sqrt{2}$ | D. | 10$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{5}{36}$ | C. | $\frac{5}{12}$ | D. | $\frac{7}{12}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com