练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    下列说法中：①经过圆柱任意两条母线的截面是一个矩形；②连结圆柱上、下底面圆周上两点的线段是圆柱的母线；③圆柱的任意两条母线互相平行；④圆柱的侧面展开图是矩形；⑤圆柱的母线有且只有一条．其中正确命题的个数为（　　）
    A、3B、1C、2D、0
    考点：命题的真假判断与应用
    专题：阅读型,空间位置关系与距离
    分析：矩形绕着它的一条边AG所在的直线旋转一周，得到的几何体，叫做圆柱，DD'不管转到任何位置，都叫母线．由定义及概念，可判断②⑤；再由性质，截面的形状，侧面展开图，即可判断①③④．
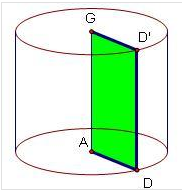    解答： 解：如图矩形绕着它的一条边AG所在的直线旋转一周，得到的几何体，叫做圆柱，DD'不管转到任何位置，都叫母线．
    故①经过圆柱任意两条母线的截面是一个矩形，则①对；
    由母线定义可知②错；由圆柱的性质可知③对；
    将圆柱沿着一条母线展开得到矩形，故④对；
    ⑤圆柱的母线有无数条，故⑤错．
    故正确的命题的个数为3，
    故选：A．
    点评：本题考查圆柱的定义，性质和侧面展开图，以及截面等概念，属于基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    图中的三角形称为希尔宾斯三角形，在下列四个三角形中，黑色三角形的个数依次构成数列{an}的前四项，依此着色方案继续对三角形着色．

    （1）数列{an}的通项公式an=
     
    ；
    （2）若数列{bn}满足bn=（
    2
    3
    ）n•an+1，记M=C
     
    0
    20
    +C
     
    1
    20
    +C
     
    2
    20
    •b1+C
     
    3
    20
    •b2+…+C
     
    20
    20
    •b19，则M的个位数字是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=
    log2x(x＞0)
    2x(x≤0)
    ，则满足f（x）=
    1
    2
    的x的值为（　　）
    A、
    		2
    或-1
    B、-1
    C、
    		2
    D、
    1
    2
    或
    		2
    或-1

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知F1，F2分别是椭圆C1和双曲线C2的公共的左右焦点，e1、e2是C1、C2的离心率，若C1、C2在第一象限内的交点为P，且满足∠POF2=2∠PF1F2，则e1、e2的关系是（　　）
    A、e12+e22=2e12e22
    B、e12+e1e2+e22=2
    C、e12+e22=2
    D、e1e2=2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，F1、F2是双曲线
    x2
    a2
    -
    y2
    24
    =1（a＞0）的左、右焦点，过F1的直线l与双曲线交于点A、B，若△ABF2为等边三角形，则△BF1F2的面积为（　　）
    A、8
    B、8
    		2
    C、8
    		3
    D、16

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    某学校随机抽查了本校20个同学，调查他们平均每天在课外从事体育锻炼的时间（分钟），根据所得数据的茎叶图，以5为组距将数据分为八组，分别是[0，5），[5，10），…[35，40]，作出的频率分布直方图如图所示，则原始的茎叶图可能是（　　）
    A、
    B、
    C、
    D、

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知“x＞2”是“x2＞a（a∈R）”的充分不必要条件，则a的取值范围是（　　）
    A、（-∞，4）
    B、（4，+∞）
    C、（0，4]
    D、（-∞，4]

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    定义在R上的函数f（x）=
    x+1
    		x2+4x+6
    ，则f（x）（　　）
    A、既有最大值也有最小值
    B、没有最大值，但有最小值
    C、有最大值，但没有最小值
    D、既没有最大值，也没有最小值

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若α，β∈R，且α≠kπ+
    π
    2
    （k∈Z），β≠kπ+
    π
    2
    （k∈Z），则“α+β=
    2π
    3
    ”是“（
    		3
    tanα-1）（
    		3
    tanβ-1）=4”的（　　）
    A、充分不必要条件
    B、必要不充分条件
    C、充要条件
    D、既不充分也不必要条件

    查看答案和解析>>

    同步练习册答案