
| 轿车A | 轿车B | 轿车C | |
| 舒适型 | 100 | 150 | z |
| 标准型 | 300 | 450 | 600 |
分析 (1)利用分层抽样满足每个个体被抽到的概率相等,列出方程求出n,再利用频数等于频率乘以样本容量求出n的值,据总的轿车数量求出z的值.
(2)先利用分层抽样满足每个个体被抽到的概率相等,求出抽取一个容量为5的样本舒适型轿车的辆数,利用列举的方法求出至少有1辆舒适型轿车的基本事件,利用古典概型的概率公式求出概率.
(3)利用平均数公式求出数据的平均数,通过列举得到该数与样本平均数之差的绝对值不超过0.5的数据,利用古典概型的概率公式求出概率.
解答 解:(1)设该厂这个月共生产轿车n辆,
由题意得$\frac{50}{n}$=$\frac{10}{100+300}$,∴n=2000,…(2分)
∴z=2000-(100+300)-150-450-600=400.…(3分)
(2)设所抽样本中有a辆舒适型轿车,
由题意,得a=2.
因此抽取的容量为5的样本中,
有2辆舒适型轿车,3辆标准型轿车.…(4分)
用A1,A2表示2辆舒适型轿车,用B1,B2,B3表示3辆标准轿车,
用E表示事件“在该样本中任取2辆,其中至少有1辆舒适型轿车”,
则基本事件空间包含的基本事件有:
(A1,A2),(A1B1),(A1B2),(A1,B3,),(A2,B1),(A2,B2)(A2,B3),
(B1B2),(B1,B3,),(B2,B3),共10个,…(6分)
事件E包含的基本事件有:(A1A2),(A1,B1,),(A1,B2),(A1,B3),
(A2,B1),(A2,B2),(A2,B3),共7个,…(8分)
故P(E)=$\frac{7}{10}$,即所求概率为$\frac{7}{10}$.…(9分)
(3)样本平均数$\overline{x}$=$\frac{1}{8}$×(9.4+8.6+9.2+9.6+8.7+9.3+9.0+8.2)=9.…(10分)
设D表示事件“从样本中任取一数,该数与样本平均数之差的绝对不超过0.5”,
则基本事件空间中有8个基本事件,…(11分)
事件D包括的基本事件有:9.4,8.6,9.2,8.7,9.3,9.0,共6个,…(13分)
∴P(D)=$\frac{6}{8}$=$\frac{3}{4}$,即所求概率为$\frac{3}{4}$.…(14分)
点评 本题考查古典概型,考查用列举法来得到事件数,考查分层抽样,是一个概率与统计的综合题目,这种题目看起来比较麻烦,但是解题的原理并不复杂.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{5}$个单位长度 | B. | 向右平移$\frac{π}{5}$个单位长度 | ||
| C. | 向左平移$\frac{π}{10}$个单位长度 | D. | 向右平移$\frac{π}{10}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{3}$或$\frac{2}{3}$π | D. | $\frac{5}{6}$π或$\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | -$\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届广西陆川县中学高三9月月考数学(文)试卷(解析版) 题型:解答题
如图,三棱柱 的侧棱
的侧棱 底面
底面 ,
,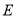 是棱
是棱 的中点,
的中点, 是
是 的中点,
的中点, .
.

(1)求证: 平面
平面 ;
;
(2)求三棱锥 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com