
分析 (1)运用数列的通项和前n项和的关系:n=1时,a1=S1,n≥2时,an=Sn-Sn-1,即可得到所求通项公式;
(2)运用数列的求和方法:错位相减法,结合等比数列的求和公式,计算即可得到所求.
解答 解:(1)n=1时,a1=S1=1;
n≥2时,an=Sn-Sn-1=$\frac{1}{2}$n(n+1)-[$\frac{1}{2}$(n-1)n]=n.
而n=1时,也满足该通项.
故综上可知:an=n;
(2)Tn=2+2•22+…+n•2n
2Tn=22+2•23+…+(n-1)•2n+n2n+1,
两式相减得:
-Tn=(2+22+23+…+2n)-n•2n+1.
即-Tn=2n+1-2-n•2n+1.
∴Tn=(n-1)2n+1+2.
点评 本题考查数列的通项和前n项和的关系,同时考查数列的求和方法:错位相减法,以及等比数列的求和公式,属于中档题.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{36}$ | B. | $\frac{1}{18}$ | C. | $\frac{1}{12}$ | D. | $\frac{1}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
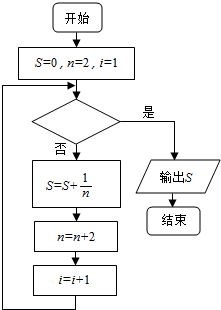 如图给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{8}+…+\frac{1}{100}$的一个程序框图,则判断框内应填入关于i的不等式为( )
如图给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{8}+…+\frac{1}{100}$的一个程序框图,则判断框内应填入关于i的不等式为( )| A. | i<50 | B. | i>50 | C. | i<51 | D. | i>51 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{33}{65}$ | B. | $\frac{63}{65}$ | C. | $\frac{33}{65}$或-$\frac{33}{65}$ | D. | -$\frac{63}{65}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 某校为了了解高三同学暑假期间学习情况,调查了200名同学,统计他们每天平均学习时间,绘成频率分布直方图(如图).则这200名同学中学习时间在6~8小时的同学为60人.
某校为了了解高三同学暑假期间学习情况,调查了200名同学,统计他们每天平均学习时间,绘成频率分布直方图(如图).则这200名同学中学习时间在6~8小时的同学为60人.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 轿车A | 轿车B | 轿车C | |
| 舒适型 | 100 | 150 | z |
| 标准型 | 300 | 450 | 600 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 甲、乙两辆汽车沿同一路线赶赴距出发地480千米的目的地,乙车比甲车晚出发2小时(从甲车出发时开始计时).图中折线OABC、线段DE分别表示甲、乙两车所行路程y(千米)与时间x(小时)之间的函数关系对应的图象(线段AB表示甲出发不足2小时因故停车检修).请根据图象所提供的信息,解决如下问题:
甲、乙两辆汽车沿同一路线赶赴距出发地480千米的目的地,乙车比甲车晚出发2小时(从甲车出发时开始计时).图中折线OABC、线段DE分别表示甲、乙两车所行路程y(千米)与时间x(小时)之间的函数关系对应的图象(线段AB表示甲出发不足2小时因故停车检修).请根据图象所提供的信息,解决如下问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com