
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | -$\frac{3}{2}$ |
分析 $\overrightarrow{OP}=(x,y)$,进行数量积的运算从而可得到$\left\{\begin{array}{l}{0≤2x+y≤1}\\{0≤y≤1}\end{array}\right.$,画出该不等式组所表示的平面区域,设z=x-y,从而有y=x-z,将该式看成在y轴上的截距为-z的直线,从而根据图形找到使-z取最大值,即使z取最小值的点,将该点坐标带入z=x-y便得到z的最小值.
解答 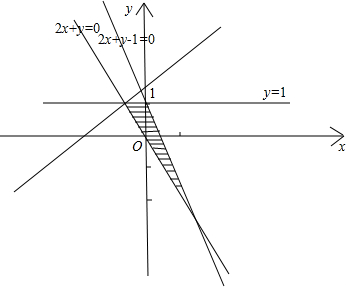 解:$\overrightarrow{OP}•\overrightarrow{OM}=2x+y$,$\overrightarrow{OP}•\overrightarrow{ON}=y$;
解:$\overrightarrow{OP}•\overrightarrow{OM}=2x+y$,$\overrightarrow{OP}•\overrightarrow{ON}=y$;
∴$\left\{\begin{array}{l}{0≤2x+y≤1}\\{0≤y≤1}\end{array}\right.$;
该不等式组表示的平面区域为下图阴影部分所示:
设z=x-y,即y=x-z;
∴当直线y=x-z的截距-z最大时,z最小;
由$\left\{\begin{array}{l}{y=1}\\{2x+y=0}\end{array}\right.$得阴影部分最左边的点为($-\frac{1}{2},1$),当y=x-z过该点时z最小;
∴$1=-\frac{1}{2}-z$;
∴z=$-\frac{3}{2}$;
即x-y的最小值为$-\frac{3}{2}$.
故选D.
点评 考查数量积的坐标运算,根据点的坐标求向量的坐标,能找出不等式组表示的平面区域,利用线性规划的知识求最值的方法.


科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 2或3 | D. | -2或-3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
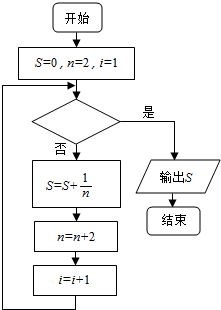 如图给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{8}+…+\frac{1}{100}$的一个程序框图,则判断框内应填入关于i的不等式为( )
如图给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{8}+…+\frac{1}{100}$的一个程序框图,则判断框内应填入关于i的不等式为( )| A. | i<50 | B. | i>50 | C. | i<51 | D. | i>51 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 某校为了了解高三同学暑假期间学习情况,调查了200名同学,统计他们每天平均学习时间,绘成频率分布直方图(如图).则这200名同学中学习时间在6~8小时的同学为60人.
某校为了了解高三同学暑假期间学习情况,调查了200名同学,统计他们每天平均学习时间,绘成频率分布直方图(如图).则这200名同学中学习时间在6~8小时的同学为60人.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 轿车A | 轿车B | 轿车C | |
| 舒适型 | 100 | 150 | z |
| 标准型 | 300 | 450 | 600 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 已知购买一张彩票中奖的概率为$\frac{1}{1000}$,则购买1000张这种彩票一定能中奖 | |
| B. | 互斥事件一定是对立事件 | |
| C. | 二进制数1101(2)转化为十进制数是13 | |
| D. | 若样本x1,x2…xn的方差为4,则样本x1-1,x2-1,…,xn-1的方差为3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -9 | B. | 9 | C. | 6 | D. | -6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com