练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知，，其中，函数的最小正周期为.

    (1)求的单调递增区间；

     (2)在中，角，，的对边分别为，，．且，，求角、、的大小．


     (1)，，

    故，                                                  ………………3分

    ，由，

    得：.

    所以的单调递增区间为．         ………………6分

     (2)因为，所以．

    因为，所以．所以．      ………………9分

    因为，，所以.             ………………12分

    因为，所以，，.                 ………………14分


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    某次文艺汇演，要将A，B，C，D，E，F这六个不同节目编排成节目单，如下表：

    序号

    1

    2

    3

    4

    5

    6

    节目

    如果A，B两个节目要相邻，且都不排在第3号位置，那么节目单上不同的排序方式有________种．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设双曲线﹣=1（a＞0，b＞0）的右焦点为F，过点F作与x轴垂直的直线l交两渐近线于A、B两点，且与双曲线在第一象限的交点为P，设O为坐标原点，若=λ+μ（λ，μ∈R），λμ=，则该双曲线的离心率为（　　）

    　

    A．

    B．

    C．

    D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在边长为1的正方形OABC中任取一点P，则点P恰好落在正方形与曲线围成的区域内（阴影部分）的概率为（　　）

    A.            B.             C.            D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


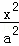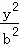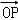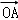    设双曲线﹣=1（a＞0，b＞0）的右焦点为F，过点F作与x轴垂直的直线l交两渐近线于A、B两点，且与双曲线在第一象限的交点为P，设O为坐标原点，若=λ+μ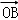（λ，μ∈R），λμ=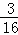，则该双曲线的离心率为（　　）

    　

    A．

    B．

    C．

    D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知AB是圆O的直径，C为圆O上一点，CD⊥AB于点D，

    弦BE与CD、AC 分别交于点M、N，且MN = MC

     

    （1）求证：MN = MB；

    （2）求证：OC⊥MN。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图所示的程序框图，该算法的功能是

    A．计算…的值

    B．计算…的值

    C．计算……的值

    D．计算……的值

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知曲线的参数方程为（为参数），在同一平面直角坐标系中，将曲线上的点按坐标变换得到曲线．

    （1）求曲线的普通方程；

    （2）若点在曲线上，点，当点在曲线上运动时，求中点的轨迹方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若存在实常数和,使得函数和对其定义域内的任意实数分别满足和，则称直线为和的“分界直线”.已知函数和函数，那么函数和函数的分界直线方程为_________.

    查看答案和解析>>

    同步练习册答案