考点:数列的求和,数列的应用
专题:等差数列与等比数列
分析:(1)由已知条件得S
n=
an2+an+,从而a
n-a
n-1=4(n≥2),又a
1=2,由此得到a
n=4n-2,从而b
1=2,
=
,由此得到
bn=2•()n-1.
(2)由c
n=
=(2n-1)•4
n-1,利用错位相减法能求出数列{c
n}的前n项的和T
n.
解答:
解:(1)∵数列{a
n}的各项均为正数,它的前n项的和为S
n,
点(a
n,S
n)在函数y=
x2+x+的图象上,
∴由已知条件得S
n=
an2+an+,①
当n≥2时,S
n-1=
an-12+an-1+,②
①-②得:
an=(an2-an-12)+(an-an-1),
即
an+an-1=(an+an-1)(an-an-1),
∵数列{a
n}的各项均为正数,∴a
n-a
n-1=4(n≥2),
又a
1=2,∴a
n=4n-2,
∵b
1=a
1,b
n+1(a
n+1-a
n)=b
n,
∴b
1=2,
=
,∴
bn=2•()n-1.
(2)∵c
n=
=(2n-1)•4
n-1,
∴T
n=1+3•4+5•4
2+…+(2n-1)•4
n-1,
4T
n=4+3•4
2+5•4
3+…+(2n-1)•4
n,
两式相减得-3T
n=1+2(4+4
2+4
3+…+4
n-1)-(2n-1)•4
n=1+2×
-(2n-1)•4
n=-
-(2n-
)•4
n,
∴T
n=
+•4n.
点评:本题主要考查数列的通项公式、前n项和公式的求法,考查等差数列、等比数列等基础知识,考查抽象概括能力,推理论证能力,运算求解能力,考查化归与转化思想、函数与方程思想,解题时要注意错位相减法的合理运用.



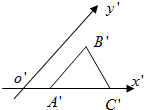 如图是水平放置的△ABC的直观图,A′B′∥y′轴,A′B′=A′C′,则△ABC是( )
如图是水平放置的△ABC的直观图,A′B′∥y′轴,A′B′=A′C′,则△ABC是( )