
设函数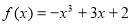 分别在
分别在 、
、 处取得极小值、极大值.
处取得极小值、极大值. 平面上点
平面上点 、
、 的坐标分别为
的坐标分别为 、
、 ,该平面上动点
,该平面上动点 满足
满足 ,点
,点 是点
是点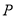 关于直线
关于直线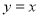 的对称点.
的对称点.
(Ⅰ)求点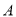 、
、 的坐标;
的坐标;
(Ⅱ)求动点 的轨迹方程.
的轨迹方程.
科目:高中数学 来源:2015届福建省高二下学期期末考试理科数学试卷(解析版) 题型:选择题
观察下列关于两个变量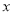 和
和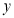 的三个散点图,它们从左到右的对应关系依次为( ).
的三个散点图,它们从左到右的对应关系依次为( ).
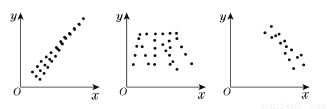
A.正相关、负相关、不相关
B.负相关、不相关、正相关
C.负相关、正相关、不相关
D.正相关、不相关、负相关
查看答案和解析>>
科目:高中数学 来源:2015届福建省高二下学期期末考理科数学试卷(解析版) 题型:选择题
某车间加工零件的数量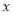 与加工时间
与加工时间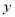 的统计数据如下表:
的统计数据如下表:
零件数 | 10 | 20 | 30 |
加工时间 | 21 | 30 | 39 |
现已求得上表数据的回归方程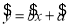 中的
中的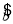 值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为
值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为
A.84分钟 B.94分钟 C.102分钟 D.112分钟
查看答案和解析>>
科目:高中数学 来源:2015届福建省高二上学期期末考理科数学试卷(解析版) 题型:选择题
若直线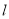 过点
过点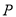 (1,0)与双曲线
(1,0)与双曲线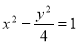 只有一个公共点,则这样的直线有
只有一个公共点,则这样的直线有
A.4条 B.3条 C. 2条 D.1条
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com