
| A. | (0,+∞) | B. | (1,+∞) | C. | (e,+∞) | D. | $(\frac{e}{3},+∞)$ |
分析 容易求出f′(0)=6,结合条件便可得出函数f(x)的解析式,进而求出导函数,代入6f(x)>f′(x),根据指数函数的单调性便可解出原不等式.
解答 解:根据条件,f(0)=1,且3f(x)=f'(x)-3,
可得3f(0)=3=f′(0)-3;
∴f′(0)=6,
由于ex的导数为ex,且由复合函数的导数法则,
可设f(x)=menx+b,可得3menx+3b=mnenx-3,
显然3b=-3,即b=-1;又3m=mn,即n=3,
由f(0)=m-1=1,即m=2,
∴f(x)=2e3x-1,f′(x)=6e3x;
∴由6f(x)>f′(x)得:6(2e3x-1)>6e3x,
整理得,e3x>1,
∴3x>0,
∴x>0.
∴原不等式的解集为(0,+∞).
故选:A.
点评 本题考查导函数的概念,基本初等函数和复合函数的求导,指数函数的单调性,考查运算能力,属于中档题.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 3$\sqrt{3}$ | B. | 6$\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | 4$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
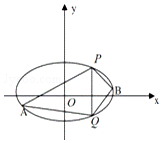 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{2}$,椭圆C的一个短轴端点与抛物线x2=4y的焦点重合.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{2}$,椭圆C的一个短轴端点与抛物线x2=4y的焦点重合.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | e2016f(-2016)<f(0),f(2016)<e2016f(0) | B. | e2016f(-2016)>f(0),f(2016)>e2016f(0) | ||
| C. | e2016f(-2016)<f(0),f(2016)>e2016f(0) | D. | e2016f(-2016)>f(0),f(2016)<e2016f(0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{\sqrt{3}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{2}$或-1 | D. | -$\frac{\sqrt{3}}{2}$或0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | b<c<a | C. | c<a<b | D. | c<b<a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com